题目内容
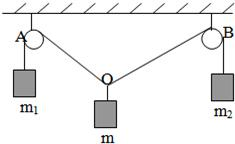 如图所示,对于同一高度(足够高)的两个定滑轮A、B,用一条足够长的绳子跨过它们,并在两端分别挂有质量为m1和m2的物体(m1≠m2),另在两滑轮中间的一段绳子的O点处悬挂质量为m的另一物体,已知m1:m2=OB:OA,且系统保持平衡(滑轮半径、绳子质量均忽略不计).求证:
如图所示,对于同一高度(足够高)的两个定滑轮A、B,用一条足够长的绳子跨过它们,并在两端分别挂有质量为m1和m2的物体(m1≠m2),另在两滑轮中间的一段绳子的O点处悬挂质量为m的另一物体,已知m1:m2=OB:OA,且系统保持平衡(滑轮半径、绳子质量均忽略不计).求证:(1)∠AOB为定值;
(2)
| m2 | m1m2 |
分析:(1)设两绳子AO、BO对物体m的拉力分别为F1、F2,物体m向下的重力为F,由系统平衡条件知F1+F2+F=0.进而设∠BAO=α,∠ABO=β,根据平行四边形法则,得F2cosβ+F1cos(π-α)=0,整理得m2cosβ-m1cosα=0,m2sinβ+m1sinα=m.进而利用正弦定理求得OB:OA=sinα:sinβ代入m2cosβ-m1cosα=0化简整理求得sin2β=sin2α.推断出2α+2β=180°.进而可知α+β=90°,则∠AOB可求.
(2)根据α+β=90°推断出cosβcosα=sinβsinα.进而利用(1)中的m2cosβ-m1cosα=0,和m2sinβ+m1sinα=m.平方后相加,进而求得m2-2m1m2>0,整理得
>2.原式得证.
(2)根据α+β=90°推断出cosβcosα=sinβsinα.进而利用(1)中的m2cosβ-m1cosα=0,和m2sinβ+m1sinα=m.平方后相加,进而求得m2-2m1m2>0,整理得
| m2 |
| m1m2 |
解答: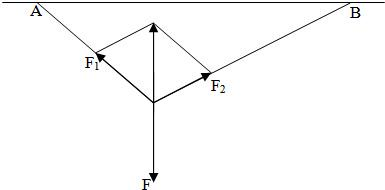 解:(1)设两绳子AO、BO对物体m的拉力分别为F1、F2,物体m向下的重力为F,由系统平衡条件知F1+F2+F=0.
解:(1)设两绳子AO、BO对物体m的拉力分别为F1、F2,物体m向下的重力为F,由系统平衡条件知F1+F2+F=0.
如图,设∠BAO=α,∠ABO=β,根据平行四边形法则,得
F2cosβ+F1cos(π-α)=0,
F2sinβ+F1sin(π-α)+F=0.
即m2cosβ-m1cosα=0,①
m2sinβ+m1sinα=m.②
在△AOB中,由正弦定理,得OB:OA=sinα:sinβ,将m1:m2=sinα:sinβ代入①,得
sinβcosβ=sinαcosα,即sin2β=sin2α.
∵m1≠m2,∴OA≠OB.∴α≠β,2α+2β=180°.
∴α+β=90°,即∠AOB=90°.
(2)由α+β=90°,得 cosβcosα=sinβsinα.
将①②平方相加,得m2=m12+m22.
由m2-2m1m2=m12+m22-2m1m2=(m1-m2)2>0,得m2>2m1m2.
∴
>2.
 解:(1)设两绳子AO、BO对物体m的拉力分别为F1、F2,物体m向下的重力为F,由系统平衡条件知F1+F2+F=0.
解:(1)设两绳子AO、BO对物体m的拉力分别为F1、F2,物体m向下的重力为F,由系统平衡条件知F1+F2+F=0.如图,设∠BAO=α,∠ABO=β,根据平行四边形法则,得
F2cosβ+F1cos(π-α)=0,
F2sinβ+F1sin(π-α)+F=0.
即m2cosβ-m1cosα=0,①
m2sinβ+m1sinα=m.②
在△AOB中,由正弦定理,得OB:OA=sinα:sinβ,将m1:m2=sinα:sinβ代入①,得
sinβcosβ=sinαcosα,即sin2β=sin2α.
∵m1≠m2,∴OA≠OB.∴α≠β,2α+2β=180°.
∴α+β=90°,即∠AOB=90°.
(2)由α+β=90°,得 cosβcosα=sinβsinα.
将①②平方相加,得m2=m12+m22.
由m2-2m1m2=m12+m22-2m1m2=(m1-m2)2>0,得m2>2m1m2.
∴
| m2 |
| m1m2 |
点评:本题主要考查了解三角形的实际应用.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
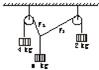 如图所示,对于同一高度(足够高)的两个定滑轮,用一条(足够长)绳子跨过它们,并在两端分别挂有4 kg和2 kg的物体,另在两个滑轮中间的一段绳子悬挂另一物体,为使系统保持平衡状态,此物体的质量应是多少?(忽略滑轮半径、绳子的重量)
如图所示,对于同一高度(足够高)的两个定滑轮,用一条(足够长)绳子跨过它们,并在两端分别挂有4 kg和2 kg的物体,另在两个滑轮中间的一段绳子悬挂另一物体,为使系统保持平衡状态,此物体的质量应是多少?(忽略滑轮半径、绳子的重量)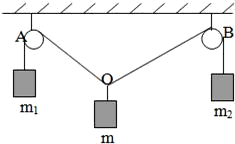 如图所示,对于同一高度(足够高)的两个定滑轮A、B,用一条足够长的绳子跨过它们,并在两端分别挂有质量为m1和m2的物体(m1≠m2),另在两滑轮中间的一段绳子的O点处悬挂质量为m的另一物体,已知m1:m2=OB:OA,且系统保持平衡(滑轮半径、绳子质量均忽略不计).求证:
如图所示,对于同一高度(足够高)的两个定滑轮A、B,用一条足够长的绳子跨过它们,并在两端分别挂有质量为m1和m2的物体(m1≠m2),另在两滑轮中间的一段绳子的O点处悬挂质量为m的另一物体,已知m1:m2=OB:OA,且系统保持平衡(滑轮半径、绳子质量均忽略不计).求证: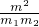 >2.
>2.