题目内容
正三棱锥的底面边长是2，侧棱长是3，则它的高h=
．
| ||
| 3 |
| ||
| 3 |
分析：由正三棱锥的底面边长是2，可以求出底面积和底面△的高；由侧棱长是3，可以求出侧面上的斜高，从而求得三棱锥的高．
解答：解：如图，在正三棱锥P-ABC中，底面边长AB=2，侧棱长PA=3，
设顶点P在底面的射影为O，连接CO并延长，交AB与点D；
连接PD，则CD⊥AB，PD⊥AB；
在正△ABC中，∵AB=2，∴CD=
，
OD=
•CD=
，
PD=
=
=2
，
∴PO=
=
=
．
故答案为：
．
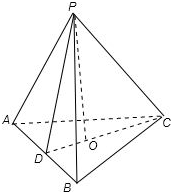
设顶点P在底面的射影为O，连接CO并延长，交AB与点D；
连接PD，则CD⊥AB，PD⊥AB；
在正△ABC中，∵AB=2，∴CD=
| 3 |
OD=
| 1 |
| 3 |
| ||
| 3 |
PD=
| PA2-AD2 |
| 9-1 |
| 2 |
∴PO=
| PD2-OD2 |
8-
|
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：题考查了三棱锥性质的应用，关键是求出三棱锥的斜高；求斜高时借助空间中垂直关系和勾股定理得出，是基础题．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南师范大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目