题目内容
已知正三棱锥的底面边长是6，侧棱与底面所成角为60°，则此三棱锥的体积为
18
| 3 |
18
．| 3 |
分析：三棱锥O-ABC的侧棱与底面ABC所成的角都是60°，故O-ABC是正三棱锥．由此入手，能够求出此三棱锥的体积．
解答：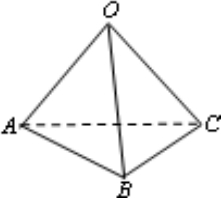
解：∵三棱锥O-ABC的侧棱与底面ABC所成的角都是60°，
∴O-ABC是正三棱锥．
过O作OG⊥平面ABC交于点G，延长AG交BC于D．
∵O-ABC是正三棱锥，
∴点G是△ABC的中心，
∴AD是等边△ABC的一条高，
∴AD=
BC=3
，
∴AG=
AD=2
．
∵OG⊥平面ABC，
∴∠ABG=60°，
∴OA=2AG=4
，OG=
AG=6．
∵△ABC是正三角形，
∴BD=CD=
BC=3，而OB=OC，∴OD⊥BD，
∴OD=
=
=
，
∴△ABC的面积=
AB2sin60°=9
．
∴O-ABC的体积为
×S△ABC×OG=18
故答案为：18
解：∵三棱锥O-ABC的侧棱与底面ABC所成的角都是60°，∴O-ABC是正三棱锥．
过O作OG⊥平面ABC交于点G，延长AG交BC于D．
∵O-ABC是正三棱锥，
∴点G是△ABC的中心，
∴AD是等边△ABC的一条高，
∴AD=
| ||
| 2 |
| 3 |
∴AG=
| 2 |
| 3 |
| 3 |
∵OG⊥平面ABC，
∴∠ABG=60°，
∴OA=2AG=4
| 3 |
| 3 |
∵△ABC是正三角形，
∴BD=CD=
| 1 |
| 2 |
∴OD=
| OB2-BD2 |
| OA2-BD2 |
| ||
| 2 |
∴△ABC的面积=
| 1 |
| 2 |
| 3 |
∴O-ABC的体积为
| 1 |
| 3 |
| 3 |
故答案为：18
| 3 |
点评：本题考查三棱锥的体积的求法，解题时要认真审题，注意合理地化立体问题为平面问题．
练习册系列答案
阅读快车系列答案
相关题目