Question

已知正三棱锥S－ABC的底面边长为a，高为h，在正三棱锥内取一点M，试求点M到底面的距离小于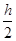的概率．

 

Answer 1

【答案】

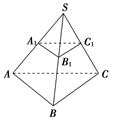
解：如图，在SA、SB、SC上取点A₁、B₁、C₁，使A₁、B₁、C₁分别为SA、SB、SC的中点，则当点M位于面ABC和面A₁B₁C₁之间时，点M到底面的距离小于.设△ABC的面积为S，由△ABC∽△A₁B₁C₁且相似比为2，得△A₁B₁C₁的面积为.由题意，三棱椎S－ABC的体积为Sh，三棱台A₁B₁C₁－ABC的体积为Sh－··＝Sh·.故P＝.

 

【解析】解：如图，在SA、SB、SC上取点A₁、B₁、C₁，使A₁、B₁、C₁分别为SA、SB、SC的中点，则当点M位于面ABC和面A₁B₁C₁之间时，点M到底面的距离小于.设△ABC的面积为S，由△ABC∽△A₁B₁C₁且相似比为2，得△A₁B₁C₁的面积为.由题意，三棱椎S－ABC的体积为Sh，三棱台A₁B₁C₁－ABC的体积为Sh－··＝Sh·.故P＝c.