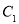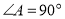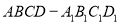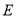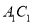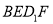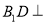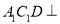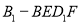题目内容
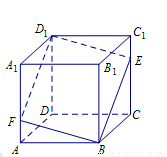
如图,在直三棱柱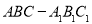 中,
中,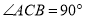 ,
,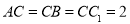 ,
,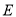 是
是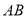 中点.
中点.

(1)求证: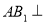 平面
平面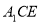 ;
;
(2)求直线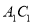 与平面
与平面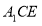 所成角的正弦值.
所成角的正弦值.
(1)参考解析;(2)
【解析】
试题分析:(1)直线与平面垂直的证明,对于理科生来说主要是以建立空间直角坐标系为主要方法,所以根据题意建立坐标系后,写出相应的点的坐标.根据向量证明向量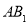 与平面内的两个相交向量的数量积为零即可.
与平面内的两个相交向量的数量积为零即可.
(2)证明直线与平面所成的角的正弦值,主要是通过求出平面的法向量与该直线的夹角的余弦值,再通过两角的互余关系转化为正弦值.
试题解析:(1)证明:因为 是直三棱柱,
是直三棱柱,
所以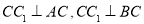 ,
,
又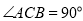 ,
,
即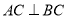 .
.
如图所示,建立空间直角坐标系 .
.

 ,
,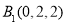 ,
, ,
, ,
,
所以 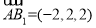 ,
, ,
,
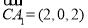 .
.
又因为  ,
,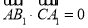 ,
,
所以  ,
,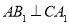 ,
,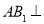 平面
平面 .
.
(2)【解析】
由(1)知, 是平面
是平面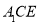 的法向量,
的法向量,
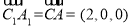 ,
,
则 
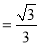 .
.
设直线 与平面
与平面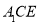 所成的角为
所成的角为 , 则
, 则
 .
.
所以直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为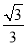 .
.
考点:1.线面垂直.2.线面所成的角.3.空间直角坐标系的解决线面问题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
在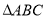 中,
中,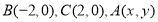 ,给出
,给出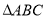 满足的条件,就能得到动点
满足的条件,就能得到动点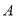 的轨迹方程,下表给出了一些条件及方程:
的轨迹方程,下表给出了一些条件及方程:
条件 | 方程 |
① |
|
② |
|
③ |
|
则满足条件①、②、③的点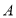 轨迹方程按顺序分别是
轨迹方程按顺序分别是
A. 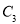 、
、 、
、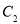 B.
B. 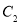 、
、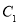 、
、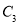
C. 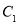 、
、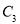 、
、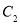 D.
D. 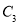 、
、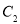 、
、