题目内容
已知m,n∈R,则“m•n<0”是“方程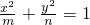 表示双曲线”的
表示双曲线”的
- A.充分不必要条件
- B.必要不充分条件
- C.充分必要条件
- D.既不充分又不必要条件
C
分析:先求出方程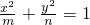 表示双曲线时m,n满足的条件,然后根据根据“谁大谁必要,谁小谁充分”的原则,若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件进行判定即可.
表示双曲线时m,n满足的条件,然后根据根据“谁大谁必要,谁小谁充分”的原则,若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件进行判定即可.
解答:∵方程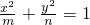 表示双曲线
表示双曲线
∴m•n<0
则“m•n<0”是“方程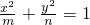 表示双曲线”的充分必要条件
表示双曲线”的充分必要条件
故选:C.
点评:本题主要考查了双曲线的标准方程以及充要条件的判定,属于基础题.判断充要条件的方法是:
①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;
②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;
③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;
④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
分析:先求出方程
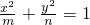 表示双曲线时m,n满足的条件,然后根据根据“谁大谁必要,谁小谁充分”的原则,若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件进行判定即可.
表示双曲线时m,n满足的条件,然后根据根据“谁大谁必要,谁小谁充分”的原则,若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件进行判定即可.解答:∵方程
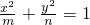 表示双曲线
表示双曲线∴m•n<0
则“m•n<0”是“方程
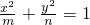 表示双曲线”的充分必要条件
表示双曲线”的充分必要条件故选:C.
点评:本题主要考查了双曲线的标准方程以及充要条件的判定,属于基础题.判断充要条件的方法是:
①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;
②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;
③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;
④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
相关题目
已知m、n∈R,则
>
成立的一个充要条件是( )
| 1 |
| m |
| 1 |
| n |
| A、m>0>n |
| B、n>m>0 |
| C、mn(m-n)<0 |
| D、m<n<0 |
已知m,n∈R,则“m•n<0”是“方程
+
=1表示双曲线”的( )
| x2 |
| m |
| y2 |
| n |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |