题目内容
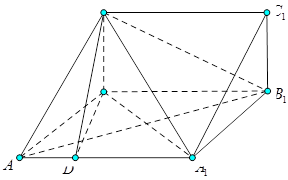
如图,在三棱柱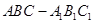 中,四边形
中,四边形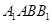 为菱形,
为菱形,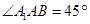 ,四边形
,四边形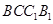 为矩形,若
为矩形,若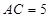 ,
,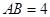 ,
,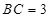 .
.
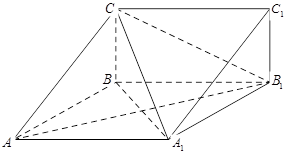
(1)求证: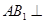 面
面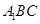 ;
;
(2)求二面角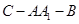 的余弦值;
的余弦值;
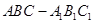 中,四边形
中,四边形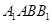 为菱形,
为菱形,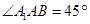 ,四边形
,四边形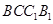 为矩形,若
为矩形,若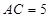 ,
,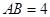 ,
,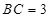 .
.
(1)求证:
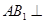 面
面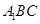 ;
;(2)求二面角
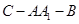 的余弦值;
的余弦值;(1)详见解析;(2)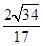 .
.
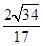 .
.试题分析:(1)先证
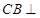 平面
平面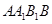 ,进而得到
,进而得到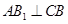 ,再由四边形
,再由四边形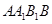 为菱形得到
为菱形得到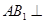
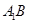 ,最后结合直线与平面垂直的判定定理证明
,最后结合直线与平面垂直的判定定理证明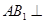 平面
平面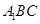 ;(2)先在平面
;(2)先在平面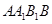 内作
内作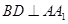 ,垂足为点
,垂足为点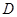 ,连接
,连接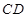 ,通过证明
,通过证明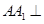 平面
平面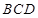 ,从而得到
,从而得到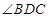 ,进而在直角三角形
,进而在直角三角形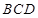 中求该角的余弦值即可.
中求该角的余弦值即可.试题解析:(1)证明:在
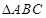 中
中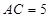 ,
,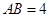 ,
,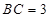 ,
,满足
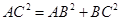 ,所以
,所以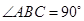 ,即
,即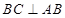 ,
,又因为四边形
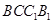 为矩形,所以
为矩形,所以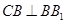 ,
,又
 ,所以
,所以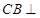 面
面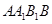 ,
,又因为
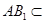 面
面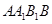 ,所以
,所以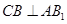 ,
, 又因为四边形
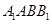 为菱形,所以
为菱形,所以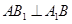 ,
,又
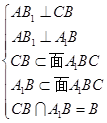 ,所以
,所以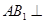 面
面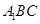 ;
;(2)过
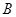 作
作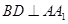 于
于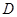 ,连接
,连接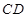 由第(1)问已证
由第(1)问已证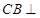 面
面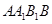 ,
,
又
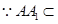 平面
平面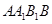 ,
,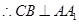 ,又
,又 ,所以
,所以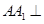 面
面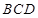 ,
,又因为
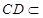 面
面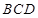 ,所以
,所以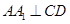 ,
,所以,
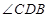 就是二面角
就是二面角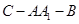 的平面角在直角
的平面角在直角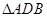 中,
中,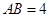 ,
,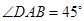 ,
,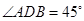 ,
,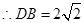 ,
,在直角
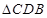 中,
中,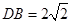 ,
,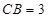 ,
,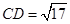 ,所以
,所以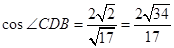 .
.
练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
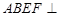 平面
平面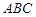 ,四边形
,四边形 为矩形,△
为矩形,△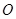 为
为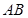 的中点,
的中点,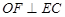 .
.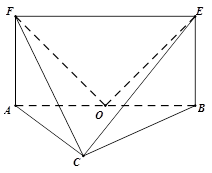
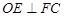 ;
; 的正切值.
的正切值.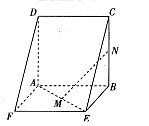
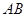 是圆的直径,
是圆的直径,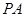 垂直圆所在的平面,
垂直圆所在的平面,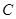 是圆上任一点,
是圆上任一点,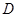 是线段
是线段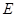 是线段
是线段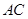 上的一点.
上的一点.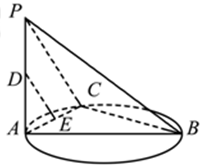
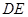 ∥平面
∥平面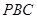 ;
;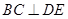 .
.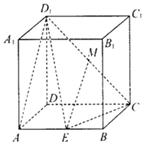
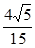 .求线段AE的长.
.求线段AE的长.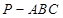 中,
中,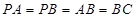 ,
,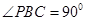 ,D为AC的中点,
,D为AC的中点,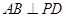 .
.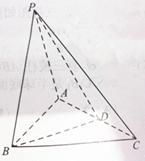
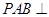 平面
平面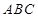 ;
;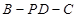 的余弦值.
的余弦值.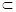 α,m
α,m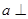 平面
平面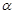 ,直线
,直线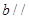 平面
平面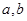 的位置关系是 .
的位置关系是 .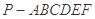 的底面是正六边形,
的底面是正六边形,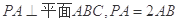 则下列结论正确的是( )
则下列结论正确的是( )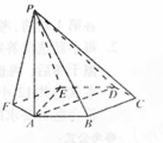


 ∥
∥
 所成的角为45°
所成的角为45°