题目内容
已知等差数列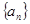 中,
中,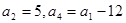 .
.
(Ⅰ)求数列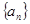 的通项公式;
的通项公式;
(Ⅱ)当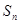 取最大值时求
取最大值时求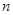 的值.
的值.
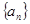 中,
中,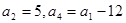 .
.(Ⅰ)求数列
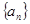 的通项公式;
的通项公式;(Ⅱ)当
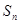 取最大值时求
取最大值时求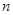 的值.
的值.(Ⅰ)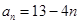 ;(Ⅱ)
;(Ⅱ)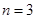 .
.
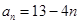 ;(Ⅱ)
;(Ⅱ)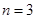 .
.试题分析:(Ⅰ)由
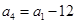 可得公差
可得公差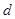 ,再由
,再由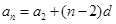 便可得通项公式.
便可得通项公式.(Ⅱ) 等差数列的前
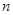 项和为关于
项和为关于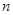 的二次式,所以求出前
的二次式,所以求出前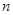 项和
项和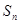 结合二次函数图象便可得其最大值及相应的
结合二次函数图象便可得其最大值及相应的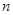 的值.
的值.试题解析:(Ⅰ)由
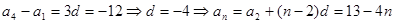 6分
6分(Ⅱ)因为
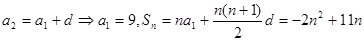 .
.对称轴为
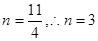 时
时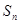 取最大值15. 13分
取最大值15. 13分 项和;2、函数的最值.
项和;2、函数的最值.
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 中,
中,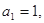 且点
且点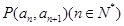 在直线
在直线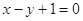 上。
上。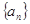 的通项公式;
的通项公式;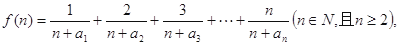 求函数
求函数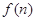 的最小值;
的最小值;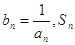 表示数列
表示数列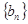 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于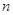 的整式
的整式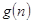 ,使得
,使得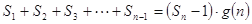 对于一切不小于2的自然数
对于一切不小于2的自然数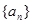 的前
的前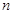 项的和为
项的和为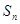 ,
, 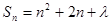 ,求证:数列
,求证:数列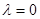 .
.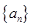 的首项为
的首项为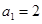 ,公比为
,公比为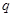 (
(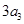 是
是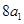 与
与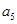 的等差中项;数列
的等差中项;数列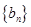 满足
满足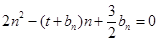 (
(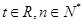 ).
).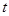 的值,使得数列
的值,使得数列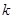 ,在
,在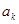 与
与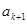 之间插入
之间插入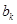 个2,得到一个新数列
个2,得到一个新数列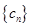 . 设
. 设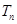 是数列
是数列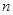 项和,试求满足
项和,试求满足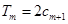 的所有正整数
的所有正整数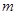 .
.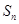 为等差数列
为等差数列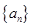 的前
的前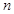 项和,且
项和,且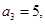
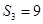 .
.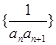 的前
的前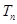 .
.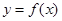 对任意的实数
对任意的实数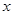 都有
都有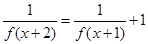 ,且
,且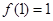 ,则
,则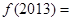
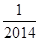

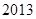
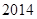
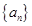 前
前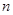 项和为
项和为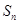 ,且
,且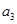 +
+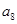 =13,
=13,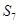 =35,则
=35,则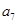 =( )
=( ) 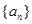 的前
的前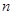 项和为
项和为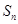 ,且
,且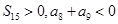 ,则使得
,则使得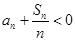 的最小的
的最小的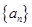 为等差数列,若
为等差数列,若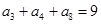 ,则
,则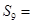 ( )
( )