题目内容
(12分)已知函数f(X)=X+2Xtan -1,X
-1,X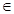 〔-1,
〔-1,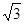 〕其中
〕其中
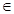 (-
(-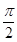 ,
,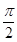 )
)
(1)当 =-
=-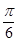 时,求函数的最大值和最小值
时,求函数的最大值和最小值
(2)求 的取值的范围,使Y=f(X)在区间〔-1,
的取值的范围,使Y=f(X)在区间〔-1,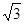 〕上是单调函数
〕上是单调函数
 -1,X
-1,X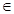 〔-1,
〔-1,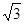 〕其中
〕其中
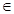 (-
(-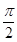 ,
,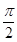 )
)(1)当
 =-
=-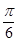 时,求函数的最大值和最小值
时,求函数的最大值和最小值(2)求
 的取值的范围,使Y=f(X)在区间〔-1,
的取值的范围,使Y=f(X)在区间〔-1,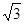 〕上是单调函数
〕上是单调函数解:(1)当 =-
=-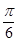 时 f(X)=
时 f(X)= -
-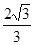 X-1=(X-
X-1=(X-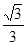 )2-
)2-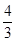
∵X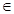 〔-1,
〔-1,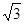 〕 ∴当X=
〕 ∴当X=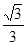 时,f(X)的最小值是 -
时,f(X)的最小值是 -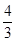
当X=-1时, f(X)的最大值是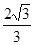
(2)f(X)=(X+tan )2-1-tan2
)2-1-tan2 是关于X的二次函数,对称轴为X=-tan
是关于X的二次函数,对称轴为X=-tan 
∵Y=f(X)在〔-1,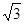 〕上是单调函数
〕上是单调函数
∴-tan ≤-1 或-tan
≤-1 或-tan  ≥
≥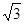
∵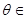 (-
(-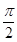 ,
,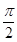 )
)
∴ 的范围是(-
的范围是(-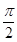 ,-
,-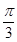 〕∪〔
〕∪〔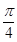 ,
,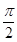 )
)
 =-
=-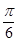 时 f(X)=
时 f(X)= -
-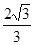 X-1=(X-
X-1=(X-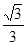 )2-
)2-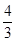
∵X
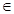 〔-1,
〔-1,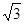 〕 ∴当X=
〕 ∴当X=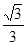 时,f(X)的最小值是 -
时,f(X)的最小值是 -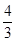
当X=-1时, f(X)的最大值是
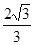
(2)f(X)=(X+tan
 )2-1-tan2
)2-1-tan2 是关于X的二次函数,对称轴为X=-tan
是关于X的二次函数,对称轴为X=-tan 
∵Y=f(X)在〔-1,
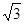 〕上是单调函数
〕上是单调函数∴-tan
 ≤-1 或-tan
≤-1 或-tan  ≥
≥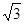
∵
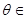 (-
(-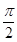 ,
,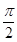 )
)∴
 的范围是(-
的范围是(-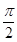 ,-
,-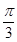 〕∪〔
〕∪〔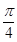 ,
,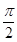 )
)略

练习册系列答案
相关题目
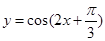 的图象,只需将函数
的图象,只需将函数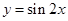 的图象( )
的图象( )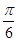 个单位
个单位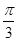 个单位
个单位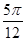 个单位
个单位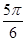 个单位
个单位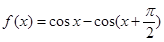 ,
,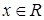
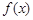 的最大值;(Ⅱ)若
的最大值;(Ⅱ)若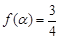 ,求
,求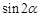 的值.
的值.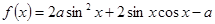 的图像
的图像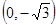 .
.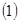 求常数
求常数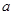 ;
;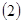 当
当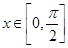 时,求函数
时,求函数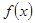 的值域.
的值域.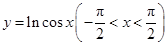 的图象是( )
的图象是( )
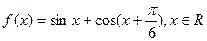 .
. 的最小正周期及其在区间
的最小正周期及其在区间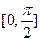 上的值域;
上的值域;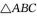 的内角A,B,C的对边分别为
的内角A,B,C的对边分别为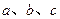 ,若
,若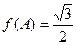 且
且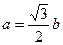 ,求角B的值.
,求角B的值.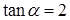 ,求
,求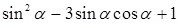 的值;
的值; 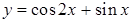 的值域.
的值域. 的周期T= ▲
的周期T= ▲ 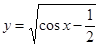 的定义域为 .
的定义域为 .