题目内容
设平面内有 条直线(
条直线(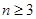 ),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用
),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用 表示这
表示这 条直线交点的个数,
条直线交点的个数,  =
=
 条直线(
条直线(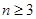 ),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用
),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用 表示这
表示这 条直线交点的个数,
条直线交点的个数,  =
=A. | B. | C. | D. |
A
试题分析:首先由图可得f(4)的值,进而逐一给出f(3),f(4),…,的值,分析可得从n-1条直线增加为n条直线时,交点的数目会增加n-1,即f(n)=f(n-1)+n-1,然后利用数列求和的办法计算可得答案. 解:如图,4条直线有5个交点,故f(4)=5,由f(3)=2,=f(4)=f(3)+3,…分析可得,从n-1条直线增加为n条直线时,交点的数目会增加n-1, f(n)=f(n-1)+n-1,累加可得f(n)=2+3+…+(n-2)+(n-1)=

故选A.
点评: 本题考查归纳推理的运用,注意运用数列的性质来发现其中的规律,并进行计算

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,
, ,且
,且 ,则
,则 中至少有一个负数”时的假设为
中至少有一个负数”时的假设为 为定点,动点
为定点,动点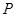 满足
满足 ,则动点
,则动点 求出
求出 猜想出数列
猜想出数列 的前
的前 项和
项和 的表达式;
的表达式; 的面积
的面积 ,猜想出椭圆
,猜想出椭圆 的面积
的面积 ;
; 的两边AB、AC互相垂直,则
的两边AB、AC互相垂直,则 。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。
。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。 是正弦函数,因此
是正弦函数,因此 是正弦函数,因此
是正弦函数,因此
 ,AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论:
,AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论: ,给出空间中三棱锥的有关结论:________
,给出空间中三棱锥的有关结论:________ ,
, ,且
,且 ,则
,则 ( )
( )


