题目内容
已知三次函数f(x)=ax3+bx2+cx+d(a,b,c,d∈R)为奇函数,且在点(1,f(1))的切线方程为y=3x-2(1)求函数f(x)的表达式.
(2)已知数列{an}的各项都是正数,且对于?n∈N*,都有(
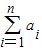 )2=
)2=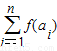 ,求数列{an}的首项a1和通项公式.
,求数列{an}的首项a1和通项公式.(3)在(2)的条件下,若数列{bn}满足bn=4n-m•2
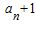 (m∈R,n∈N*),求数列{bn}的最小值.
(m∈R,n∈N*),求数列{bn}的最小值.
【答案】分析:(1)由奇函数性质得f(-x)=-f(x)恒成立,由此可求得b,d,根据点(1,f(1))处的切线方程为y=3x-2,可得f′(1)=3,f(1)=1,解出即可;
(2):(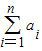 )2=
)2=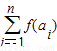 ,即为
,即为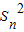 =
=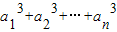 ①,令n=1可求得首项a1,当n≥2时,
①,令n=1可求得首项a1,当n≥2时,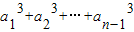 =
=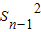 ②,①-②并化简可得
②,①-②并化简可得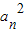 =2Sn-an③,依此可得
=2Sn-an③,依此可得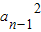 =2Sn-1-an-1④,由③-④可得递推式,据此可判断数列为等差数列,从而可求得通项公式;
=2Sn-1-an-1④,由③-④可得递推式,据此可判断数列为等差数列,从而可求得通项公式;
(3)由(2)易求得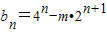 =(2n-m)2-m2(n∈N+),令2n=t(t≥2),则bn变为关于t的二次函数形式,在t≥2范围内对m进行分类讨论,注意t为大于等于2的正整数;
=(2n-m)2-m2(n∈N+),令2n=t(t≥2),则bn变为关于t的二次函数形式,在t≥2范围内对m进行分类讨论,注意t为大于等于2的正整数;
解答:解:(1)∵f(x)=ax3+bx2+cx+d(a、b、c、d∈R)为奇函数,
∴f(-x)=-f(x)恒成立,∴-ax3+bx2-cx+d=-(ax3+bx2+cx+d),
∴b=d=0,
∴f(x)=ax3+cx,
∴f'(x)=3ax2+c,
∵点(1,f(1))处的切线方程为y=3x-2,
∴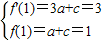 ,解得a=1,c=0,
,解得a=1,c=0,
∴f(x)=x3;
(2)由题意可知:(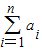 )2=
)2=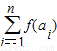 ,
,
∴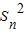 =
=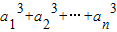 ①,
①,
由①式可得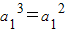 ,
,
∵a1>0,∴a1=1,
当n≥2时,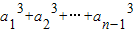 =
=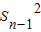 ②,
②,
由①-②可得: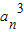 =
=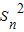 -
-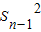 =an(Sn+Sn-1),
=an(Sn+Sn-1),
∵数列{an}的各项都是正数,
∴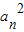 =Sn+Sn-1=2Sn-an③,
=Sn+Sn-1=2Sn-an③,
∴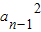 =2Sn-1-an-1④,
=2Sn-1-an-1④,
由③-④可得: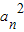 -
-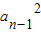 =an+an-1,
=an+an-1,
∵an+an-1>0,∴an-an-1=1,
∴数列{an}是以首项为1,公差为1的等差数列,
∴an=n;
(3)∵an=n,∴bn=4n-m•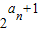 ,∴
,∴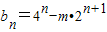 =(2n-m)2-m2(n∈N+),
=(2n-m)2-m2(n∈N+),
令2n=t(t≥2),∴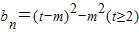 ,
,
(i)当m≤2时,数列{bn}的最小值为当n=1时,bn=4-4m.
(ii)当m>2时,
①若m=2k(k∈N+,k≥2)时,数列{bn}的最小值为当n=k时,bk=-m2,
②若m=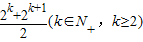 时,数列{bn}的最小值为,当n=k时或n=k+1,
时,数列{bn}的最小值为,当n=k时或n=k+1,
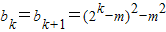 ,
,
③若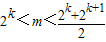 (k∈N+,k≥2)时,数列{bn}的最小值为,当n=k时,
(k∈N+,k≥2)时,数列{bn}的最小值为,当n=k时,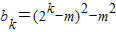 ,
,
④若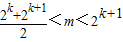 (k∈N+,k≥2)时,数列{bn}的最小值为,当n=k+1时,
(k∈N+,k≥2)时,数列{bn}的最小值为,当n=k+1时,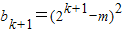 -m2.
-m2.
点评:本题考查数列与函数的综合、函数奇偶性的性质,考查学生综合运用所学知识分析问题解决问题的能力,本题综合性强,能力要求较高.
(2):(
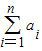 )2=
)2=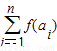 ,即为
,即为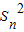 =
=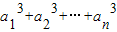 ①,令n=1可求得首项a1,当n≥2时,
①,令n=1可求得首项a1,当n≥2时,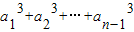 =
=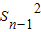 ②,①-②并化简可得
②,①-②并化简可得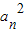 =2Sn-an③,依此可得
=2Sn-an③,依此可得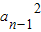 =2Sn-1-an-1④,由③-④可得递推式,据此可判断数列为等差数列,从而可求得通项公式;
=2Sn-1-an-1④,由③-④可得递推式,据此可判断数列为等差数列,从而可求得通项公式;(3)由(2)易求得
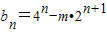 =(2n-m)2-m2(n∈N+),令2n=t(t≥2),则bn变为关于t的二次函数形式,在t≥2范围内对m进行分类讨论,注意t为大于等于2的正整数;
=(2n-m)2-m2(n∈N+),令2n=t(t≥2),则bn变为关于t的二次函数形式,在t≥2范围内对m进行分类讨论,注意t为大于等于2的正整数;解答:解:(1)∵f(x)=ax3+bx2+cx+d(a、b、c、d∈R)为奇函数,
∴f(-x)=-f(x)恒成立,∴-ax3+bx2-cx+d=-(ax3+bx2+cx+d),
∴b=d=0,
∴f(x)=ax3+cx,
∴f'(x)=3ax2+c,
∵点(1,f(1))处的切线方程为y=3x-2,
∴
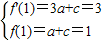 ,解得a=1,c=0,
,解得a=1,c=0,∴f(x)=x3;
(2)由题意可知:(
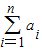 )2=
)2=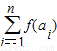 ,
,∴
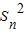 =
=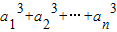 ①,
①,由①式可得
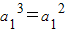 ,
,∵a1>0,∴a1=1,
当n≥2时,
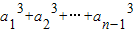 =
=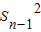 ②,
②,由①-②可得:
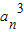 =
=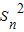 -
-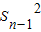 =an(Sn+Sn-1),
=an(Sn+Sn-1),∵数列{an}的各项都是正数,
∴
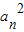 =Sn+Sn-1=2Sn-an③,
=Sn+Sn-1=2Sn-an③,∴
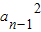 =2Sn-1-an-1④,
=2Sn-1-an-1④,由③-④可得:
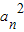 -
-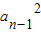 =an+an-1,
=an+an-1,∵an+an-1>0,∴an-an-1=1,
∴数列{an}是以首项为1,公差为1的等差数列,
∴an=n;
(3)∵an=n,∴bn=4n-m•
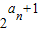 ,∴
,∴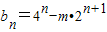 =(2n-m)2-m2(n∈N+),
=(2n-m)2-m2(n∈N+),令2n=t(t≥2),∴
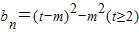 ,
,(i)当m≤2时,数列{bn}的最小值为当n=1时,bn=4-4m.
(ii)当m>2时,
①若m=2k(k∈N+,k≥2)时,数列{bn}的最小值为当n=k时,bk=-m2,
②若m=
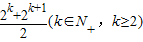 时,数列{bn}的最小值为,当n=k时或n=k+1,
时,数列{bn}的最小值为,当n=k时或n=k+1,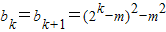 ,
,③若
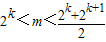 (k∈N+,k≥2)时,数列{bn}的最小值为,当n=k时,
(k∈N+,k≥2)时,数列{bn}的最小值为,当n=k时,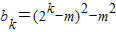 ,
,④若
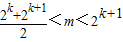 (k∈N+,k≥2)时,数列{bn}的最小值为,当n=k+1时,
(k∈N+,k≥2)时,数列{bn}的最小值为,当n=k+1时,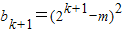 -m2.
-m2.点评:本题考查数列与函数的综合、函数奇偶性的性质,考查学生综合运用所学知识分析问题解决问题的能力,本题综合性强,能力要求较高.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知三次函数f(x)=ax3+bx2+cx+d的图象如图所示,则
已知三次函数f(x)=ax3+bx2+cx+d的图象如图所示,则