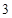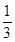题目内容
已知函数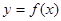 是定义在实数集R上的奇函数,且当
是定义在实数集R上的奇函数,且当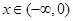 时
时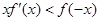 成立(其中
成立(其中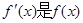 的导函数),若
的导函数),若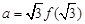 ,
,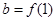 ,
,
则 的大小关系是( )
的大小关系是( )
A.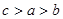 | B.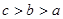 |
C.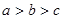 | D.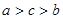 |
A
解析试题分析:由题意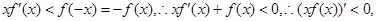 所以
所以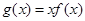 是
是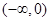 上的减函数,而
上的减函数,而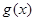 是偶函数,所以
是偶函数,所以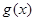 是
是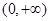 上的增函数, 而
上的增函数, 而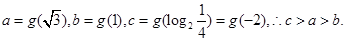
考点:本小题主要考查函数的奇偶性和单调性的综合应用,考查利用导数研究单调性以及利用单调性比较函数值的大小,考查学生的逻辑推理能力和综合运用所学知识解决问题的能力.
点评:解决本小题的关键在于由已知条件得出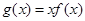 的单调性,解决综合性问题时一定要灵活,要想方设法将待求解问题向熟悉的数学问题上转化.
的单调性,解决综合性问题时一定要灵活,要想方设法将待求解问题向熟悉的数学问题上转化.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
对于R上可导的任意函数f(x),若满足(x-1)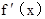 ³0,则必有( )
³0,则必有( )
| A.f(0)+f(2)<2f(1) | B.f(0)+f(2)£2f(1) |
| C. f(0)+f(2)³2f(1) | D.f(0)+f(2)>2f(1) |
如果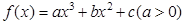 导函数图像的顶点坐标为
导函数图像的顶点坐标为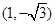 ,那么曲线
,那么曲线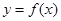 上任一点的切线的倾斜角
上任一点的切线的倾斜角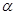 的取值范围是( )
的取值范围是( )
A.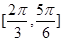 | B.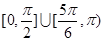 |
C.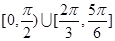 | D.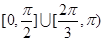 |
若函数 的导函数
的导函数 ,则函数
,则函数 的单调递减区间是( )
的单调递减区间是( )
A.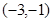 | B.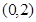 | C. | D.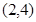 |
已知定义在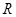 上的函数
上的函数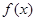 满足
满足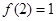 ,且
,且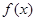 的导函数
的导函数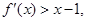 则不等式
则不等式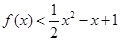 的解集为( )
的解集为( )
A.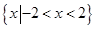 | B.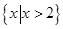 | C.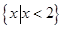 | D.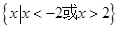 |
设函数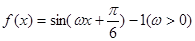 的导函数
的导函数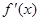 的最大值为3,则
的最大值为3,则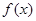 的图象的一条对称轴的方程是( )
的图象的一条对称轴的方程是( )
A.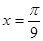 | B.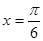 | C.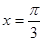 | D.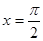 |
已知函数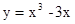 ,则它的单调减区间是
,则它的单调减区间是
| A.(-∞,0) | B.(0,+ ∞) |
| C.(-1,1) | D.(-∞,-1)和(1,+ ∞) |
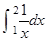 等于
等于
| A.-2ln2 | B.2ln2 | C.-ln2 | D.ln2 |