题目内容
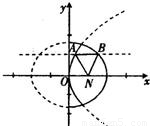
 定点N(1,0),动点A、B分别在图中抛物线y2=4x及椭圆
定点N(1,0),动点A、B分别在图中抛物线y2=4x及椭圆 的实线部分上运动,且AB∥x轴,则△NAB的周长l取值范围是( )
的实线部分上运动,且AB∥x轴,则△NAB的周长l取值范围是( )A.(
 )
)B.(
 )
)C.(
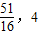 )
)D.(2,4)
【答案】分析:根据抛物线和椭圆的方程可知准线方程分别为x=-1和x=4,分别过点A、B作AA1⊥l2于A1,BB1⊥l1于B1,根据抛物线和椭圆的性质可知|BN|=e|BB1|和|AN|=|AA1|,代入△NAB的周长|AN|+|AB|+|BN|中,根据抛物线和椭圆的交点及椭圆的右端点可确定B点的横坐标的范围,进而确定周长的范围.
解答:解:分别作出椭圆准线l1:x=4与抛物线的准线l2:x=-1,分别过点A、B作AA1⊥l2于A1,BB1⊥l1于B1,
由椭圆的第二定义可得|BN|=e|BB1|=2- xB,由抛物线定义可得|AN|=|AA1|=xA+1,
xB,由抛物线定义可得|AN|=|AA1|=xA+1,
∴△NAB的周长=|AN|+|AB|+|BN|=xA+1+(xB-xA)+2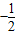 xB=3+
xB=3+ xB,
xB,
又由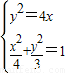 ,可得两曲线交点的横坐标为x=
,可得两曲线交点的横坐标为x= ,
,
∵xB∈( ,2),∴3+
,2),∴3+ xB∈(
xB∈(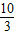 ,4),
,4),
即△NAB的周长l的取值范围为(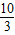 ,4),
,4),
故选B.
点评:本题主要考查了椭圆和抛物线性质.要利用好椭圆的第一和第二定义及抛物线的定义.
解答:解:分别作出椭圆准线l1:x=4与抛物线的准线l2:x=-1,分别过点A、B作AA1⊥l2于A1,BB1⊥l1于B1,
由椭圆的第二定义可得|BN|=e|BB1|=2-
 xB,由抛物线定义可得|AN|=|AA1|=xA+1,
xB,由抛物线定义可得|AN|=|AA1|=xA+1,∴△NAB的周长=|AN|+|AB|+|BN|=xA+1+(xB-xA)+2
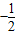 xB=3+
xB=3+ xB,
xB,又由
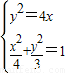 ,可得两曲线交点的横坐标为x=
,可得两曲线交点的横坐标为x= ,
,∵xB∈(
 ,2),∴3+
,2),∴3+ xB∈(
xB∈(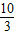 ,4),
,4),即△NAB的周长l的取值范围为(
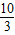 ,4),
,4),故选B.
点评:本题主要考查了椭圆和抛物线性质.要利用好椭圆的第一和第二定义及抛物线的定义.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
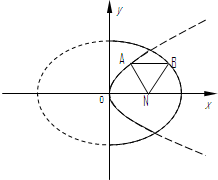 定点N(1,0),动点A、B分别在图中抛物线y2=4x及椭圆
定点N(1,0),动点A、B分别在图中抛物线y2=4x及椭圆| x2 |
| 4 |
| y2 |
| 3 |
A、(
| ||
B、(
| ||
C、(
| ||
| D、(2,4) |
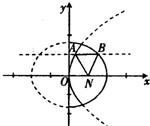 已知定点N(1,0),动点A、B分别在图中抛物线y2=4x及椭圆
已知定点N(1,0),动点A、B分别在图中抛物线y2=4x及椭圆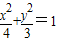 的实线部分上运动,且AB∥x轴,则△NAB的周长L的取值范围是
的实线部分上运动,且AB∥x轴,则△NAB的周长L的取值范围是 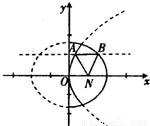
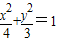 的实线部分上运动,且AB∥x轴,则△NAB的周长L的取值范围是
的实线部分上运动,且AB∥x轴,则△NAB的周长L的取值范围是