题目内容
13.在△ABC中,角A,B,C的对边分别为a,b,c,且a+c=$\sqrt{2}b$.(Ⅰ)若a=c,求角B;
(Ⅱ)若accosB=2,b=2$\sqrt{3}$,求△ABC的面积.
分析 (Ⅰ)由条件利用正弦定理求得cosA=$\frac{\sqrt{2}}{2}$,可得A=$\frac{π}{4}$,进而求得sinB=$\sqrt{2}$sinA 的值,可得B的值.
(Ⅱ)由条件利用余弦定理求得ac和B的值,可得△ABC的面积为$\frac{1}{2}$ac•sinB 的值.
解答 解:(Ⅰ)在△ABC中,由a+c=$\sqrt{2}b$,a=c,可得 2sinA=$\sqrt{2}$sinB,即sinB=$\sqrt{2}$sinA,
即sin(π-2A)=$\sqrt{2}$sinA,即2sinAcosA=$\sqrt{2}$sinA,求得cosA=$\frac{\sqrt{2}}{2}$,可得A=$\frac{π}{4}$,∴sinB=$\sqrt{2}$sinA=1,
∴B=$\frac{π}{2}$.
(Ⅱ)若accosB=2,b=2$\sqrt{3}$,则由余弦定理可得b2=12=a2+c2-2ac•cosB=(a+c)2-2ac-4=2b2-2ac-4=24-2ac-4,
求得ac=4,代入accosB=2,求得cosB=$\frac{1}{2}$,∴B=$\frac{π}{3}$,
∴△ABC的面积为$\frac{1}{2}$ac•sinB=2•$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
点评 本题主要考查正弦定理和余弦定理的应用,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
4.i是虚数单位,$\overrightarrow{z}$表示复数z的共轭复数,若$\overrightarrow{z}=1+i$,则$\frac{\overrightarrow{z}}{i}+i•z$=( )
| A. | -2 | B. | 2 | C. | -2i | D. | 2i |
7.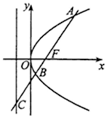 如图,过抛物线y2=2px(p>0)焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )
如图,过抛物线y2=2px(p>0)焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )
 如图,过抛物线y2=2px(p>0)焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )
如图,过抛物线y2=2px(p>0)焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )| A. | y2=3x | B. | y2=9x | C. | y2=$\frac{3}{2}$x | D. | y2=$\frac{9}{2}$x |