题目内容
已知等差数列{an}的公差为-2，a3是a1与a4的等比中项，则首项a1=________，前n项和Sn=________．
8 -n2+9n
分析：由题意可得（a1-4）2=a1•（a1-6），解之可得a1，代入求和公式可得Sn．
解答：由题意可得（a1-4）2=a1•（a1-6），
解得a1=8，故Sn=na1+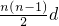
=8n-n2+n=-n2+9n
故答案为：8；-n2+9n
点评：本题考查等差数列的前n项和公式和等比中项的定义，属基础题．
分析：由题意可得（a1-4）2=a1•（a1-6），解之可得a1，代入求和公式可得Sn．
解答：由题意可得（a1-4）2=a1•（a1-6），
解得a1=8，故Sn=na1+
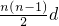=8n-n2+n=-n2+9n故答案为：8；-n2+9n
点评：本题考查等差数列的前n项和公式和等比中项的定义，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知等差数列{an}中，a4a6=-4，a2+a8=0，n∈N*．