题目内容
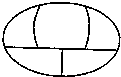
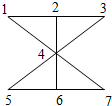
把3盆不同的兰花和4盆不同的玫瑰花摆放在如图图案中的1，2，3，4，5，6，7所示的位置上，其中三盆兰花不能放在一条直线上，则不同的摆放方法为______种．
由题意，七盆花总的摆放种数为A77=5040，
三盆兰花在一条直线上的种数要分三步来完成，第一步，取线共有C51种，第二步摆放兰花共有A33种，第三步摆放玫瑰花共有A44种
故兰花在一条直线上的摆放种数为C51×A33×A44=720
其中三盆兰花不能放在一条直线上的不同的摆放方法为5040-720=4320
故答案为4320
三盆兰花在一条直线上的种数要分三步来完成，第一步，取线共有C51种，第二步摆放兰花共有A33种，第三步摆放玫瑰花共有A44种
故兰花在一条直线上的摆放种数为C51×A33×A44=720
其中三盆兰花不能放在一条直线上的不同的摆放方法为5040-720=4320
故答案为4320
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
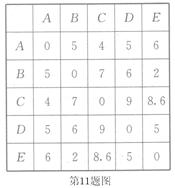
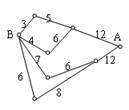
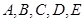五个城市间进行，各城市之间的路线距离（单位：百公里）见右表. 若以
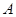为起点，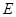
为终点，每个城市经过且只经过一次，那么火炬传递的最短路线距离为（ ）
