题目内容
若函数y=x2-3x-4的定义域为[0,m],值域为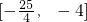 ,则m的取值范围是
,则m的取值范围是
- A.(0,4]
- B.
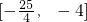
- C.
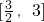
- D.
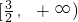
C
分析:先配方利用定义域值域,分析确定m的范围.
解答:y=x2-3x-4=x2-3x+ -
- =(x-
=(x- )2-
)2-
定义域为〔0,m〕
那么在x=0时函数值最大
即y最大=(0- )2-
)2- =
= -
- =-4
=-4
又值域为〔- ,-4〕
,-4〕
即当x=m时,函数最小且y最小=-
即- ≤(m-
≤(m- )2-
)2- ≤-4
≤-4
0≤(m- )2≤
)2≤
即m≥ (1)
(1)
即(m- )2≤
)2≤
m- ≥-3
≥-3 且m-
且m- ≤
≤
0≤m≤3 (2)
所以: ≤m≤3
≤m≤3
故选C.
点评:本题考查函数的定义域值域的求法,是中档题.
分析:先配方利用定义域值域,分析确定m的范围.
解答:y=x2-3x-4=x2-3x+
 -
- =(x-
=(x- )2-
)2-
定义域为〔0,m〕
那么在x=0时函数值最大
即y最大=(0-
 )2-
)2- =
= -
- =-4
=-4又值域为〔-
 ,-4〕
,-4〕即当x=m时,函数最小且y最小=-

即-
 ≤(m-
≤(m- )2-
)2- ≤-4
≤-40≤(m-
 )2≤
)2≤
即m≥
 (1)
(1)即(m-
 )2≤
)2≤
m-
 ≥-3
≥-3 且m-
且m- ≤
≤
0≤m≤3 (2)
所以:
 ≤m≤3
≤m≤3故选C.
点评:本题考查函数的定义域值域的求法,是中档题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目