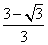题目内容
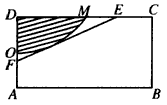
如图,有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到D的距离都等于它到边AB的距离,工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1米,AD=0.5米,问如何画切割线EF可使五边形ABCEF的面积最大?
| 解:由条件易知,边缘线OM是以点D为焦点, 直线AB为准线的抛物线的一部分, 以O点为原点,AD所在直线为,y轴建立如图所示的平面直角坐标系, 则  , ,易求得边缘线OM所在的抛物线的方程为 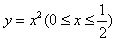 , ,要使如图的五边形ABCEF的面积最大,则必有EF所在直线与抛物线相切, 设切点为P(t,t2),则直线EF的方程为y=2t(x-t)+t2,即y=2tx-t2, 由此可得 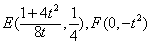 , ,∴ 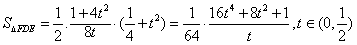 , ,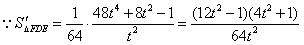 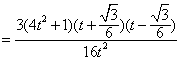 , ,显然函数 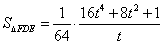 在 在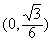 上是减函数, 上是减函数,在 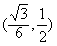 上是增函数, 上是增函数,∴当 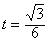 时,S△FDE取得最小值,相应地,五边形ABCEF的面积最大, 时,S△FDE取得最小值,相应地,五边形ABCEF的面积最大,此时 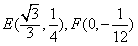 , ,即沿直线EF画线段切割可使五边形ABCEF的面积最大。 |
 |

练习册系列答案
相关题目
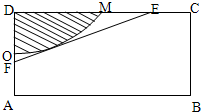 如图,有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1米,AD=0.5米,当沿切割线EF切割使剩余部分五边形ABCEF的面积最大时,AF的长度为( )米.
如图,有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1米,AD=0.5米,当沿切割线EF切割使剩余部分五边形ABCEF的面积最大时,AF的长度为( )米.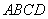 缺损了一角(图中阴影部分),边缘线
缺损了一角(图中阴影部分),边缘线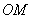 上每一点到点
上每一点到点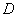 的距离都等于它到边
的距离都等于它到边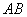 的距离。工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若
的距离。工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若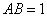 米,
米,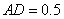 米,当沿切割线
米,当沿切割线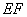 切割使剩余部分五边形
切割使剩余部分五边形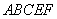 的面积最大时,
的面积最大时,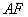 的长度为( )米。
的长度为( )米。 A
A
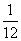 B
B
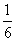
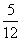 D
D