题目内容
已知数列{an}共有m项,记{an}的所有项和为S(1),第二项及以后所有项和为S(2),第三项及以后所有项和为S(3),…,第n项及以后所有项和为S(n),若S(n)是首项为1,公差为2的等差数列的前n项和,则当n<m时,an = .
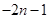
解析试题分析:依题意可知S(n)和S(n+1),进而根据an=S(n)-S(n+1)求得答案.解:∵n<m,∴m≥n+1,又S(n)=n×1+ × 2=n2,∴S(n+1)=(n+1)2,故an=S(n)-S(n+1)=n2-(n+1)2=-2n-1,故答案为:-2n-1
× 2=n2,∴S(n+1)=(n+1)2,故an=S(n)-S(n+1)=n2-(n+1)2=-2n-1,故答案为:-2n-1
考点:等差数列前n项和
点评:本题主要考查等差数列前n项和公式.属基础题.

练习册系列答案
相关题目
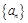 为等差数列,且
为等差数列,且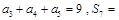 .
. 行第
行第 列的数为
列的数为 ,则
,则
 ;
; 的前
的前 项和是
项和是 ,若
,若 ,
, ,则
,则 的值为
的值为 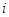 行第
行第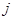 列的数记为
列的数记为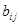 (
(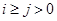 ),则
),则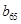 = .
= .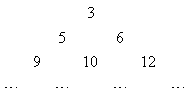
 中,al =" l," a2 =" 2+3" , a3 =" 4+5+6" , a4 =" 7+8+9+10" , ……,则a10的值是_______
中,al =" l," a2 =" 2+3" , a3 =" 4+5+6" , a4 =" 7+8+9+10" , ……,则a10的值是_______ 为等差数列,
为等差数列, ,
, ,则
,则 ___________.
___________. 的前10项和为30,则
的前10项和为30,则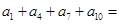 ___________.
___________.