题目内容
已知下列几个命题: ①已知F1、F2为两定点, =4,动点M满足
=4,动点M满足 ,则动点M的轨迹是椭圆。 ②一个焦点为
,则动点M的轨迹是椭圆。 ②一个焦点为 且与双曲线
且与双曲线 有相同的渐近线的双曲线标准方程是
有相同的渐近线的双曲线标准方程是 ③“若
③“若 =b,则a2=ab”的否命题。④若一个动圆的圆心在抛物线
=b,则a2=ab”的否命题。④若一个动圆的圆心在抛物线 上,且动圆恒与直线
上,且动圆恒与直线 相切,则动圆必过定点
相切,则动圆必过定点 。
。
其中真命题有____________
【答案】
②④
【解析】
试题分析:①已知F1、F2为两定点,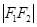 =4,动点M满足
=4,动点M满足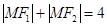 ,则动点M的轨迹是椭圆。不对,轨迹是线段
,则动点M的轨迹是椭圆。不对,轨迹是线段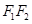 ;
;
②一个焦点为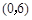 且与双曲线
且与双曲线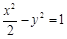 有相同的渐近线的双曲线标准方程是
有相同的渐近线的双曲线标准方程是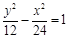 ,正确,因为,双曲线的焦点为
,正确,因为,双曲线的焦点为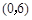 ,与双曲线
,与双曲线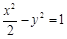 有相同的渐近线,即
有相同的渐近线,即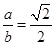 ,由
,由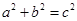 得,双曲线标准方程是
得,双曲线标准方程是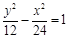 ;
;
③“若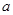 =b,则a2=ab”的否命题。不对。若
=b,则a2=ab”的否命题。不对。若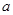 =b,则a2=ab”的否命题是:若a2
=b,则a2=ab”的否命题是:若a2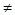 ab,则
ab,则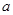
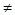 b,表示真命题;
b,表示真命题;
④若一个动圆的圆心在抛物线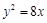 上,且动圆恒与直线
上,且动圆恒与直线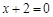 相切,则动圆必过定点
相切,则动圆必过定点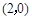 。正确。∵抛物线y2=8x的准线方程为x=-2,∴由题可知动圆的圆心在y2=8x上,且恒与抛物线的准线相切,由定义可知,动圆恒过抛物线的焦点(2,0)。
。正确。∵抛物线y2=8x的准线方程为x=-2,∴由题可知动圆的圆心在y2=8x上,且恒与抛物线的准线相切,由定义可知,动圆恒过抛物线的焦点(2,0)。
故答案为②④。
考点:圆锥曲线的定义、标准方程、几何性质,命题及其否命题。
点评:中档题,本题综合性较强,较全面地考查圆锥曲线的定义、标准方程、几何性质,命题及其否命题。对考生灵活解题的能力要求较高。

练习册系列答案
相关题目