题目内容
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去,则a2009+a2010+a2011等于( )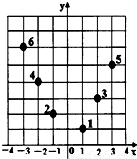
A.1003
B.1005
C.1006
D.2011
【答案】分析:根据题目所给的六个点的坐标把十二个数字写出来,组成数列的前十二项,观察数列的特点,所有偶数项项,项是项数的一半,第二、六、十项前后两项互为相反数,而要求的2010在2、6、10组成的数列里.
解答:解:∵所有偶数项,项是项数的一半,
∴a2010=1005,
∵二、六、十项前后两项互为相反数,而要求的2010在2、6、10组成的数列里.
∴a2009+a2011=0,
故选B
点评:有的数列可以通过实际事件构造新数列,构造出一个我们较熟悉的数列,从而求出数列的通项公式.这类问题考查学生的灵活性,考查学生分析问题及运用知识解决问题的能力,这是一种化归能力的体现.
解答:解:∵所有偶数项,项是项数的一半,
∴a2010=1005,
∵二、六、十项前后两项互为相反数,而要求的2010在2、6、10组成的数列里.
∴a2009+a2011=0,
故选B
点评:有的数列可以通过实际事件构造新数列,构造出一个我们较熟悉的数列,从而求出数列的通项公式.这类问题考查学生的灵活性,考查学生分析问题及运用知识解决问题的能力,这是一种化归能力的体现.

练习册系列答案
相关题目
 18、如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横纵坐标分别对应数列{an}(n∈N*)的前12项,如下表所示:
18、如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横纵坐标分别对应数列{an}(n∈N*)的前12项,如下表所示: 12、如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去,则a2009+a2010+a2011等于( )
12、如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去,则a2009+a2010+a2011等于( ) 14、如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横纵坐标分别对应数列{an} (n∈N*)的前12项,如下表所示:
14、如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横纵坐标分别对应数列{an} (n∈N*)的前12项,如下表所示:
 如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:编号为1,2,3,4,5,6的横纵坐标分别对应数列{an)(n∈N*)的前12项,如下表所示,
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:编号为1,2,3,4,5,6的横纵坐标分别对应数列{an)(n∈N*)的前12项,如下表所示, (n∈Z*)的前12项,
(n∈Z*)的前12项,


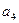






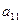













 = ▲ .
= ▲ .