题目内容
在△ABC中,cos(A+C)=-
,且a,c的等比中项为
.
(1)求△ABC的面积;
(2)若a=7,求角C.
| 3 |
| 5 |
| 35 |
(1)求△ABC的面积;
(2)若a=7,求角C.
分析:(1)由条件求得sinB=
,cosB=
,ac=35,再由△ABC的面积为
•ac•sinB,运算求得结果.
(2)由a=7,可得c=5,由余弦定理可得 b2=32,可得b=4
.再由正弦定理求得sinC=
,从而求得C的值.
| 4 |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
(2)由a=7,可得c=5,由余弦定理可得 b2=32,可得b=4
| 2 |
| ||
| 2 |
解答:解:(1)在△ABC中,cos(A+C)=-
,可得sin(A+C)=sinB=
,∴cosB=
.
再由a,c的等比中项为
可得ac=35,故△ABC的面积为
•ac•sinB=14.
(2)∵a=7,∴c=5,由余弦定理可得 b2=a2+c2-2ac•cosB=49+25-70×
=32,
∴b=4
.
再由正弦定理可得
=
,即
=
,∴sinC=
,∴C=
.
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
再由a,c的等比中项为
| 35 |
| 1 |
| 2 |
(2)∵a=7,∴c=5,由余弦定理可得 b2=a2+c2-2ac•cosB=49+25-70×
| 3 |
| 5 |
∴b=4
| 2 |
再由正弦定理可得
| c |
| sinC |
| b |
| sinB |
| 5 |
| sinC |
4
| ||
|
| ||
| 2 |
| π |
| 4 |
点评:本题主要考查正弦定理、余弦定理的应用,等比中项的定义,根据三角函数的值求角.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
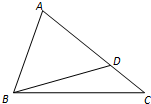 如图,在△ABC中,cos∠ABC=
如图,在△ABC中,cos∠ABC=