题目内容
已知函数f(x)=
满足f(1)=1,f(2)=
.(1)求f(x)的表达式;
(2)判断F(x)= lg［f(x)］在x∈［-1，1］上的单调性，并用定义给出证明;
(3)若m∈R，求F(|m- 
|-|m+
|)的值域.
解析：（1）由已知
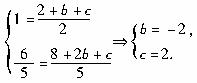
（2）由（1）知
设-1≤x1＜x2≤1,
?
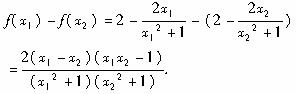
因为x12+1＞0,x22+1＞0,x1-x2＜0,x1x2-1＜0,所以f(x1) -f(x2)＞0,即f(x)在［-1，1］上单调递减.又?|
|≤|
|=1,?
所以f(x)＞0, lg［f(x)］有意义.?
所以F(x)=lg［f(x)］在［-1，1］上单调递减.??
（3）||m-
|-|m+
||≤|m-
-(m+
)|= 
,
所以-
≤|m-
|-|m+
|≤
.
所以F(
)≤F(|m-
|-|m+
|)≤F(-
).?
而F(
)=lg
,F(-
)=lg
,?
所以所求值域为［lg
,lg
］.
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）为R上的连续函数且存在反函数f-1（x），若函数f（x）满足下表：
那么，不等式|f-1（x-1）|＜2的解集是（ ）
那么，不等式|f-1（x-1）|＜2的解集是（ ）
A、{x|
| ||
B、{x|
| ||
| C、{x|1＜x＜2} | ||
| D、{x|1＜x＜5} |
(x≠－1)．设数列{an}满足a1＝1，an+1＝f(an)，数列{bn}满bn＝|an－
|，Sn＝b1＋b2＋…＋bn(n∈N*)
；
．