题目内容
已知一扇形的中心角是α,所在圆的半径是R.(1)若α=60°,R=10 cm,求扇形的弧所在的弓形面积;
(2)若扇形的周长是一定值c(c>0),当α为多少弧度时,该扇形有最大面积?
【答案】分析:(1)直接求出扇形的面积,求出三角形的面积,然后求出扇形的弧所在的弓形面积;
(2)法一:通过周长关系式,化简扇形的面积公式,得到关于α的表达式,利用基本不等式解答即可.
法二:通过周长关系式,化简扇形的面积公式,得到关于弧长l的表达式,利用二次函数的最值求出最大值,以及圆心角解答即可.
解答:解:(1)设弧长为l,弓形面积为S弓,
∵α=60°= ,R=10,∴l=
,R=10,∴l=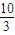 π(cm),
π(cm),
S弓=S扇-S△= ×
×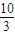 π×10-
π×10- ×102×sin60°
×102×sin60°
=50(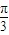 -
-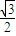 )(cm2).
)(cm2).
(2)法一:∵扇形周长c=2R+l=2R+αR,
∴R=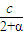 ,
,
∴S扇= α•R2=
α•R2= α(
α(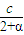 )2=
)2=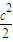 α•
α•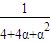
=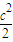 •
•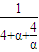 ≤
≤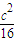 .
.
∴当且仅当α=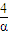 ,即α=2(α=-2舍去)时,扇形面积有最大值
,即α=2(α=-2舍去)时,扇形面积有最大值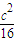 .
.
法二:由已知2R+l=c,∴R=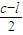 (l<c),
(l<c),
∴S= Rl=
Rl= •
•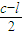 •l=
•l= (cl-l2)
(cl-l2)
=- (l-
(l-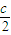 )2+
)2+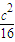 ,
,
∴当l=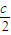 时,Smax=
时,Smax=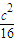 ,此时α=
,此时α=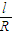 =
=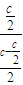 =2,
=2,
∴当扇形圆心角为2弧度时,扇形面积有最大值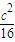 .
.
点评:本题是基础题,考查扇形的面积公式的应用,基本不等式以及二次函数的应用,利用基本不等式求最值需要满足“正、定、等”的条件;二次函数注意x的范围;考查计算能力.
(2)法一:通过周长关系式,化简扇形的面积公式,得到关于α的表达式,利用基本不等式解答即可.
法二:通过周长关系式,化简扇形的面积公式,得到关于弧长l的表达式,利用二次函数的最值求出最大值,以及圆心角解答即可.
解答:解:(1)设弧长为l,弓形面积为S弓,
∵α=60°=
 ,R=10,∴l=
,R=10,∴l=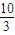 π(cm),
π(cm),S弓=S扇-S△=
 ×
×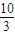 π×10-
π×10- ×102×sin60°
×102×sin60°=50(
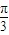 -
-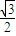 )(cm2).
)(cm2).(2)法一:∵扇形周长c=2R+l=2R+αR,
∴R=
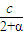 ,
,∴S扇=
 α•R2=
α•R2= α(
α(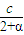 )2=
)2=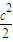 α•
α•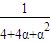
=
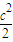 •
•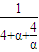 ≤
≤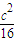 .
.∴当且仅当α=
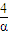 ,即α=2(α=-2舍去)时,扇形面积有最大值
,即α=2(α=-2舍去)时,扇形面积有最大值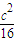 .
.法二:由已知2R+l=c,∴R=
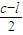 (l<c),
(l<c),∴S=
 Rl=
Rl= •
•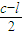 •l=
•l= (cl-l2)
(cl-l2)=-
 (l-
(l-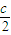 )2+
)2+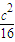 ,
,∴当l=
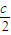 时,Smax=
时,Smax=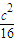 ,此时α=
,此时α=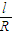 =
=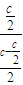 =2,
=2,∴当扇形圆心角为2弧度时,扇形面积有最大值
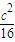 .
.点评:本题是基础题,考查扇形的面积公式的应用,基本不等式以及二次函数的应用,利用基本不等式求最值需要满足“正、定、等”的条件;二次函数注意x的范围;考查计算能力.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
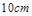 ,当扇形的圆心角a为多少弧度时,该扇形面积有最大面积 ?
,当扇形的圆心角a为多少弧度时,该扇形面积有最大面积 ?