题目内容
对![]() ,不等式
,不等式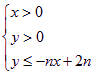 所表示的平面区域为
所表示的平面区域为![]() ,把
,把![]() 内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成一列点:
内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成一列点:![]()
(1)求![]() ,
,![]()
(2)若![]() (
(![]() 为非零常数),问是否存在整数
为非零常数),问是否存在整数![]() ,使得对任意
,使得对任意![]() ,
,
都有![]() .
.
(1)![]() (2)存在
(2)存在![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]()
解析:
解:(1)![]() ,又
,又![]() 且
且![]() ,∴
,∴![]() ……(1分)
……(1分)
故![]() 内的整点都落在直线
内的整点都落在直线![]() 上且
上且![]() ,故
,故![]() 内的整点按其到原点的距离从近到远排成的点列为:
内的整点按其到原点的距离从近到远排成的点列为:![]() ,∴
,∴![]() ……(5分)
……(5分)
(2)![]() ,
,
∴![]()
![]()
∴![]() ……(*) ……(8分)
……(*) ……(8分)
当![]() 时,(*)式即为
时,(*)式即为![]() 对
对![]() 都成立,∴
都成立,∴![]()
……(10分)
当![]() 时,(*)式即为
时,(*)式即为![]() 对
对![]() 都成立,∴
都成立,∴![]()
……(12分)
∴![]() ,又
,又![]() 且
且![]() ,
,
∴存在![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() . ……(14分)
. ……(14分)

练习册系列答案
相关题目
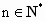 ,不等式
,不等式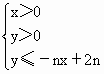 所表示的平面区域为
所表示的平面区域为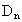 ,把
,把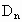 内的整点(横坐标与纵坐标均为整数点)按其到原点的距离从近到远排成点列:
内的整点(横坐标与纵坐标均为整数点)按其到原点的距离从近到远排成点列:
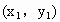
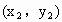 ,
,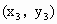 ,…,
,…,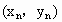 .
.
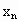 ,
,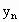 ;
;
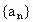 满足
满足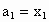 ,且
,且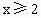 时
时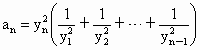 .证明:当
.证明:当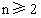 时,
时,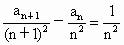 .
.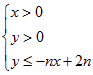 所表示的平面区域为
所表示的平面区域为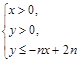 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列(x1,y1),(x2,y2),?,(xn,yn),
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列(x1,y1),(x2,y2),?,(xn,yn),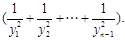 证明:当n≥2时,
证明:当n≥2时,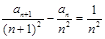 ;
;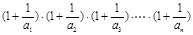 与4的大小关系.
与4的大小关系.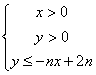 所表示的平面区域为
所表示的平面区域为