Question

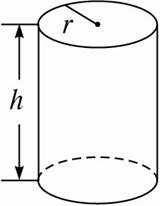
圆柱形金属饮料罐的容积一定时,它的高与底半径应怎样选取,才能使所用材料最省?

Answer 1

思路分析：列函数关系式,利用导数求最值.

解：如上图，设圆柱的高为h,底面半径为R,则表面积

S=2πRh+2πR²,

由V=πR²h,得h=,则S(R)=2πR·+2πR²=+2πR².

令S′(R)=+4πR=0,得R=,

从而h==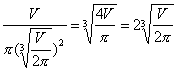,即h=2R,

所以当罐的高与底直径相等时,所用材料最省.

    深化升华 在实际问题中,有时会遇到在区间内只有一个点使f′(x)=0,如函数在这点有极值,那么不与端点值比较,也可以知道这就是最值,也适用于开区间或无穷区间.