Question

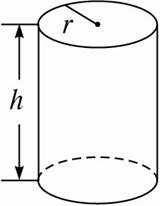
圆柱形金属饮料罐的容积一定时，它的高与底半径应怎样选取才能使所用材料最省？

Answer 1

思路分析：解这类有关函数最大值、最小值的实际问题时，首先要把各个变量用字母表示出来，然后需要分析问题中各个变量之间的关系，找出适当的函数关系式，并确定函数的定义区间；接着运用数学知识求解，所得结果要符合问题的实际意义.也就是说最后要进行检验.这里要使用料最省，就是使圆柱形的表面积最小，并且体积一定.

解：设圆柱的高为h,底半径为R，则表面积S=2πRh+2πR².

∵V=πR²h,∴h=.?

∴S=S（R）=2πR·+2πR²=+2πR².

∵S′=S′（R）=-+4πR,令-+4πR=0,即4πR³-2V=0.

解得R=

∴h=====，

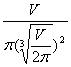即h=2R.

∵当0＜R＜时，S′＜0.

当R＞时，S′＞0.

∴S（R）在R=处有极小值，?

且S_极小值=6π.

∵S（R）只有一个极值，故是最小值.

答：当罐的高与底的直径相等时，所用材料最省.

温馨提示

在实际问题中，有时会遇到在区间内只有一个点使f′（x）=0，如函数在这点有极值，那么不与端点值比较，也可以知道这就是最值，也适用于开区间或无穷区间.