题目内容
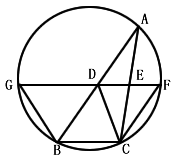
（选做题）如图，D，E分别为△ABC边AB，AC的中点，直线DE交△ABC的外接圆于F，G两点，若CF∥AB。
证明：（1）CD=BC；
（2）△BCD～△GBD。
（2）△BCD～△GBD。
证明：（1）∵D，E分别为△ABC边AB，AC的中点
∴DE∥BC
∵CF∥AB，
∴四边形BCFD是平行四边形
∴CF=BD=AD
∵CF∥AD 连接AF，则四边形ADCF是平行四边形，
∴CD=AF
∵FG∥BC，∴GB=CF
∴BD=CF，
∴GB=BD
∴∠DGB=∠BDG
∵CF∥AB，
∴AF=BC
∵AF=CD，
∴BC=CD，
（2）由（1）知∠DBC=∠BDC
∵∠EFC=∠DBC=∠DGB
∴∠DGB=∠DBC，∠GDB=∠BDC
∴△BCD～△GBD 。
∴DE∥BC
∵CF∥AB，
∴四边形BCFD是平行四边形
∴CF=BD=AD
∵CF∥AD 连接AF，则四边形ADCF是平行四边形，
∴CD=AF
∵FG∥BC，∴GB=CF
∴BD=CF，
∴GB=BD
∴∠DGB=∠BDG
∵CF∥AB，
∴AF=BC
∵AF=CD，
∴BC=CD，
（2）由（1）知∠DBC=∠BDC
∵∠EFC=∠DBC=∠DGB
∴∠DGB=∠DBC，∠GDB=∠BDC
∴△BCD～△GBD 。
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
（2012•咸阳三模）（考生注意：请在下列三道试题中任选一题作答，如果多做，则按所做的第一题评阅记分）
（2013•肇庆一模）（几何证明选讲选做题）
