题目内容
(本题满分12分) 已知函数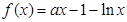
 .
.
(1)讨论函数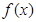 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)若函数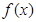 在
在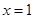 处取得极值,对
处取得极值,对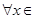
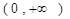 ,
,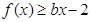 恒成立,求实数
恒成立,求实数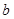 的取值范围;
的取值范围;
(3)当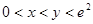 且
且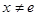 时,试比较
时,试比较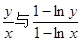 的大小.
的大小.
【答案】
(1)当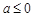 时
时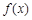 在
在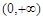 上没有极值点,
上没有极值点,
当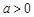 时,
时,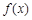 在
在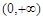 上有一个极值点(2)
上有一个极值点(2)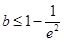 (3)当0<x<e时
(3)当0<x<e时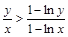 ,当e<x<e2时
,当e<x<e2时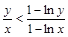
【解析】
试题分析:(Ⅰ)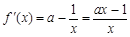 ,当
,当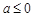 时,
时,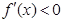 在
在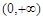 上恒成立,函数
上恒成立,函数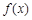 在
在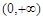 单调递减,∴
单调递减,∴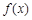 在
在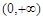 上没有极值点;
上没有极值点;
当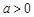 时,
时,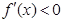 得
得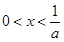 ,
,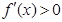 得
得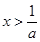 ,
,
∴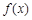 在
在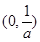 上递减,在
上递减,在 上递增,即
上递增,即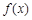 在
在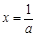 处有极小值.
处有极小值.
∴当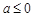 时
时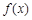 在
在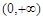 上没有极值点,
上没有极值点,
当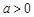 时,
时,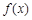 在
在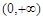 上有一个极值点.-----3分
上有一个极值点.-----3分
(Ⅱ)∵函数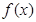 在
在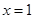 处取得极值,∴
处取得极值,∴ ,
,
∴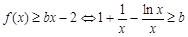 ,---------5分
,---------5分
令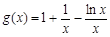 ,可得
,可得 在
在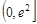 上递减,在
上递减,在 上递增,
上递增,
∴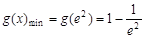 ,即
,即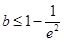 .------- 7分
.------- 7分
(Ⅲ)由(Ⅱ)知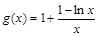 在(0,e2)上单调减
在(0,e2)上单调减
∴0<x<y<e2时,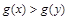 即
即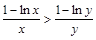
当0<x<e时,1-lnx>0,∴y(1-lnx)>x(1-lny), ∴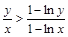
当e<x<e2时,1-lnx<0,∴y(1-lnx)>x(1-lny), ∴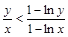 -----12分
-----12分
考点:利用函数的导数求极值最值单调区间
点评:不等式恒成立问题常转化为求函数最值问题。

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面