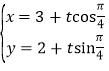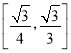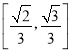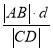题目内容
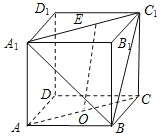
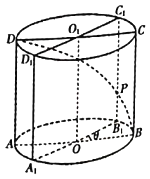
【题目】如图,已知圆柱![]() ,底面半径为1,高为2,
,底面半径为1,高为2,![]() 是圆柱的一个轴截面,动点
是圆柱的一个轴截面,动点![]() 从点
从点![]() 出发沿着圆柱的侧面到达点
出发沿着圆柱的侧面到达点![]() ,其路径最短时在侧面留下的曲线记为
,其路径最短时在侧面留下的曲线记为![]() :将轴截面
:将轴截面![]() 绕着轴
绕着轴![]() ,逆时针旋转
,逆时针旋转![]()
![]() 角到
角到![]() 位置,边
位置,边![]() 与曲线
与曲线![]() 相交于点
相交于点![]() .
.
(1)当![]() 时,求证:直线
时,求证:直线![]() 平面
平面![]() ;
;
(2)当![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)法一:建立如图所示的空间直角坐标系,写出各点坐标,求得平面![]() 的法向量,可得结论;
的法向量,可得结论;
法二:由已知条件推导出AB⊥A1B1,AB⊥OO1,得到AB⊥平面A1B1C1D1,可得AB⊥B1D1,结合OP⊥B1D1由此能证明直线B1D1⊥平面PAB.
(2)以![]() 所在直线为
所在直线为![]() 轴,过点
轴,过点![]() 与
与![]() 垂直的直线为
垂直的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴建立空间直角坐标系,分别求得两个面的法向量,利用向量法能求出二面角D﹣AB﹣P的余弦值.
轴建立空间直角坐标系,分别求得两个面的法向量,利用向量法能求出二面角D﹣AB﹣P的余弦值.
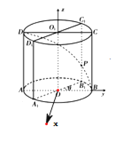
(1)方法一:当![]() 时,建立如图所示的空间直角坐标系,
时,建立如图所示的空间直角坐标系,
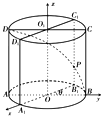
则有![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,
,
可取![]() ,得
,得![]() ,
,![]() ,
,![]() .
.
所以直线![]() 平面
平面![]() .
.
方法二:在正方形![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() ,
,
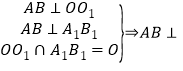 平面
平面![]() ,又
,又![]() 平面
平面![]()
所以![]() ,又
,又![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]()
所以直线![]() 平面
平面![]() .
.
(2)当![]() 时,以
时,以![]() 所在直线为
所在直线为![]() 轴,过点
轴,过点![]() 与
与![]() 垂直的直线为
垂直的直线为![]() 轴,
轴, 所在的直线为
所在的直线为![]() 轴建立如图空间直角坐标系,
轴建立如图空间直角坐标系,![]()
可得![]() ,所以
,所以![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则
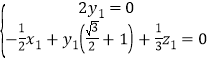 ,可取
,可取![]() ,得
,得![]() ,
,
又平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则![]()
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】随着科技的发展,近年看电子书的国人越来越多;所以近期有许多人呼呼“回归纸质书”,目前出版物阅读中纸质书占比出现上升现随机选出200人进行采访,经统计这200人中看纸质书的人数占总人数![]() .将这200人按年龄分成五组:第l组
.将这200人按年龄分成五组:第l组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,其中统计看纸质书的人得到的频率分布直方图如图所示.
,其中统计看纸质书的人得到的频率分布直方图如图所示.
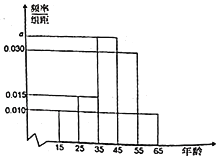
(1)求![]() 的值及看纸质书的人的平均年龄;
的值及看纸质书的人的平均年龄;
(2)按年龄划分,把年龄在![]() 的称青壮年组,年龄在
的称青壮年组,年龄在![]() 的称为中老年组,若选出的200人中看电子书的中老年人有10人,请完成下面
的称为中老年组,若选出的200人中看电子书的中老年人有10人,请完成下面![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下认为看书方式与年龄层有关?
列联表,并判断能否在犯错误的概率不超过0.1的前提下认为看书方式与年龄层有关?
看电子书 | 看纸质书 | 合计 | |
青壮年 | |||
中老年 | |||
合计 |
附:![]() (其中
(其中![]() ).
).
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |