题目内容
2.设x,y,z为整数且x+y+z=3,x3+y3+z3=3,则x2+y2+z2=3或57.分析 设x=1+a,y=1+b,z=1+c,可得a+b+c=0.代入x3+y3+z3=3,可得:a3+b3+c3+3(a2+b2+c2)=0,利用a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-bc-ac),可得:a3+b3+c3-3abc=0.可得a2+b2+c2=-abc,且abc≤0.于是x2+y2+z2=a2+b2+c2+3=3-abc.①若a,b,c有一个为0,那么x2+y2+z2=3 (此时a=b=c=0显然满足条件).②若a,b,c有两正一负,不妨设a≥b>0>c,2(a2+ab+b2)=ab(a+b),设ab=u,a+b=v.化简整理即可得出.
解答 解:设x=1+a,y=1+b,z=1+c,∵x+y+z=3,
那么a+b+c=0.
代入x3+y3+z3=3,
可得:a3+b3+c3+3(a2+b2+c2)=0,
∵a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-bc-ac),
可得:a3+b3+c3-3abc=0.
∴a2+b2+c2=-abc,且abc≤0.
∵x2+y2+z2=a2+b2+c2+2(a+b+c)+3=a2+b2+c2+3=3-abc,
①若a,b,c有一个为0,那么x2+y2+z2=3 (此时a=b=c=0显然满足条件).
②若a,b,c有两正一负,不妨设a≥b>0>c,
2(a2+ab+b2)=ab(a+b),
设ab=u,a+b=v.
那么2v2-2u=uv,化为2v2=u(v+2),
∴u=$\frac{2{v}^{2}}{v+2}$=2(v-2)+$\frac{8}{v+2}$.
∵v=a+b>0,
∴v的可取值为2,6.
此时u为4,9.
∴a+b=2,ab=4或a+b=6,ab=9.
此时有整数解a=3,b=3,c=-6,
对应x=4,y=4,z=-5.
此时x2+y2+z2=57.
∴x2+y2+z2=57或3.
点评 本题考查了乘法公式的应用、换元方法、分类讨论方法,考查了变形能力与计算能力,属于难题.

| A. | c>b>a | B. | a>b>c | C. | c>a>b | D. | b>c>a |
| A. | 3l-2m+$\frac{1}{3}n$ | B. | 3l-2m-$\frac{1}{3}n$ | C. | 3l-2m+3n | D. | 3l-2m-3n |
90 71 64 66 72 39 49 46 55 56 85 52 6l
80 66 67 78 70 51 65 42 73 77 58 67

(Ⅰ)请根据数据在答题卡的茎叶图中完成物理成绩统计;
(Ⅱ)请根据数据在答题卡上完成数学成绩的频数分布表及数学成绩的频率分布直方图;
| 数学成绩分组 | [50,60﹚ | [60,70﹚ | [70,80﹚ | [80,90﹚ | [90,100﹚ | [100,110﹚ | [110,120] |
| 频数 |

(Ⅲ)设上述样本中第i位考生的数学、物理成绩分别为xi,yi(i=1,2,3,…,25).通过对
样本数据进行初步处理发现:数学、物理成绩具有线性相关关系,得到:
$\overline{x}$=$\frac{1}{25}$$\sum_{i=1}^{25}$xi=86,$\overline{y}$=$\frac{1}{25}$$\sum_{i=1}^{25}$yi=64,$\sum_{i=1}^{25}$(xi-$\overline{x}$)(yi-$\overline{y}$)=4698,$\sum_{i=1}^{25}$(xi-$\overline{x}$)2=5524,$\frac{4698}{5524}$≈0.85.
求y关于x的线性回归方程,并据此预测当某考生的数学成绩为100分时,该考生的物理成绩(精确到1分).
附:回归直线方程的斜率和截距的最小二乘估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}\overline{x}$.
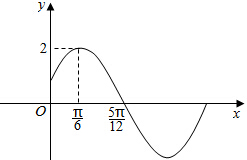 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.