题目内容
已知f(x)=ax2+bx+3a+b是偶函数,且其定义域为[a-1,2a],则y=f(x)的最大值为( )
A.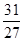 |
| B.1 |
C. |
| D.2 |
A
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义在R上的函数f(x)满足f(x)= ,则f(3)的值为( )
,则f(3)的值为( )
| A.-1 | B.-2 | C.1 | D.2 |
函数 的零点所在的区间是( )
的零点所在的区间是( )
A. | B. | C.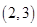 | D. |
已知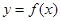 是定义在R上的偶函数,且在[0,+
是定义在R上的偶函数,且在[0,+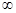 )上单调递增,则满足f(m)<f(1)的实数m的范围是
)上单调递增,则满足f(m)<f(1)的实数m的范围是
A.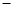 l<m<0 l<m<0 |
| B.0<m<1 |
C.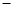 l<m<1 l<m<1 |
D.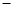 l≤m≤1 l≤m≤1 |
已知函数 的值域为[0,+∞),若关于x的不等式f(x)<c的解集为(m,m+6),则实数c的值为( )
的值域为[0,+∞),若关于x的不等式f(x)<c的解集为(m,m+6),则实数c的值为( )
| A.7 |
| B.8 |
| C.9 |
| D.10 |
设函数g(x)=x2-2(x∈R),f(x)=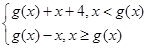 则f(x)的值域是( )
则f(x)的值域是( )
A.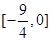 ∪(1,+∞) ∪(1,+∞) |
| B.[0,+∞) |
C.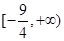 |
D.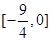 ∪(2,+∞) ∪(2,+∞) |
函数 的定义域是( )
的定义域是( )
A. |
B. |
C. |
D. |
已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增.若实数a满足f(log2a)+ ≤2f(1),则a的取值范围是 ( )
≤2f(1),则a的取值范围是 ( )
| A.[1,2] |
B. |
C. |
| D.(0,2] |
设 为定义在R上的奇函数,当
为定义在R上的奇函数,当 时,
时, (b为常数),则
(b为常数),则 ( )
( )
| A.3 |
| B.1 |
C. |
D. |