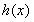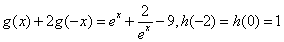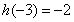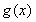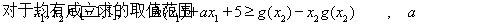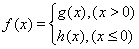题目内容
(13分)(1)二次函数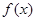 满足:
满足: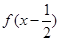 为偶函数且
为偶函数且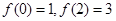 ,求
,求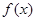 的解析式;
的解析式;
(2)若函数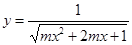 定义域为
定义域为 ,求
,求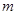 取值范围。
取值范围。
(3)若函数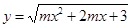 值域为
值域为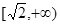 ,求
,求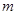 取值范围。
取值范围。
(4)若函数 在
在 上单调递减,求
上单调递减,求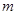 取值范围。
取值范围。
【答案】
(1)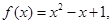 (2)
(2)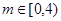 ;(3)
;(3)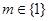 ;(4)
;(4)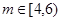 。
。
【解析】本试题主要是考查了函数的奇偶性以及函数的概念和单调性的运用。
(1)要使函数定义域为R,则分母中x无论取何值,根号下都是正数,对于参数m=0,m>0两种情况来讨论得到
(2)因为值域给出,那么利用函数的单调性可知,根号下的范围是大于等于2,然后利用对于参数m讨论得到。
(3)因为函数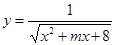 在
在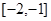 上单调递减,那么利用单调性的性质可知,分母递增函数,结合二次函数的
对称轴得到范围。
上单调递减,那么利用单调性的性质可知,分母递增函数,结合二次函数的
对称轴得到范围。

练习册系列答案
相关题目