题目内容
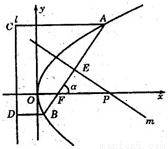
如图,倾斜角为a的直线经过抛物线y2=8x的焦点F,且于抛物线交于A、B两点.(Ⅰ)求抛物线的焦点F的坐标及准线l的方程
(Ⅱ)若a为锐角,作线段AB的垂线平分m交x轴于点P,证明|FP|-|FP|cos2a为定值,并求此定值.

【答案】分析:(Ⅰ)根据抛物线的方程可求得抛物线标准方程中的p,则焦点坐标和准线方程可得.
(Ⅱ)设出A,B的坐标,和M的坐标,把A,B代入抛物线方程两式相减求得直线AB的斜率,求得yotana=4.同时根据AB,MP共线根据斜率相等求得得yotana=4,进而可推断出AB中垂线方程的斜率,表示出其直线方程,令y=0表示出P的横坐标,进而可表示出|FP|,然后利用余弦的二倍角公式化简整理,把tana= ,yo2=4xo-8代入整理求得结果为8,为定值,进而原式得证.
,yo2=4xo-8代入整理求得结果为8,为定值,进而原式得证.
解答: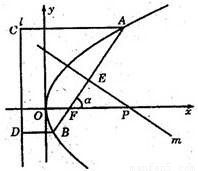 解:(Ⅰ)抛物线方程中p=4,
解:(Ⅰ)抛物线方程中p=4,
∴焦点坐标为(2,0),准线方程为x=-2
(Ⅱ)设A(x1,y1),B(x2,y2),AB中点E(xo,yo),焦点F(2,0).
则有x1+x2=2xo,y1+y2=2yo,又A,B在曲线上有y12=8x1,y22=8x2,
两式相减得AB斜率k=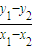 =
=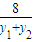 =
= =tana,得yotana=4.
=tana,得yotana=4.
又AB,MP共线,易得AB中垂线方程y=-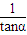 (x-xo)+yo,令y=0,
(x-xo)+yo,令y=0,
得P点横坐标xP=xo+yotana=xo+4.
于是得|FP|=xP-xF=xo+2.
由于1-cos2a=1-(cos2a-sin2a)=1-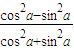 =1-(1-
=1-(1-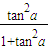 ),
),
再将tana= ,yo2=4xo-8代入整理得1-cos2a=
,yo2=4xo-8代入整理得1-cos2a=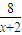 ,
,
从而有|PF|-|PF|cos2a=|PF|(1-cos2a)=(xo+2)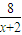 =8.
=8.
原式得证.
点评:本题主要考查了抛物线的应用,平面解析式的基础知识.考查了考生的基础知识的综合运用和知识迁移的能力.
(Ⅱ)设出A,B的坐标,和M的坐标,把A,B代入抛物线方程两式相减求得直线AB的斜率,求得yotana=4.同时根据AB,MP共线根据斜率相等求得得yotana=4,进而可推断出AB中垂线方程的斜率,表示出其直线方程,令y=0表示出P的横坐标,进而可表示出|FP|,然后利用余弦的二倍角公式化简整理,把tana=
 ,yo2=4xo-8代入整理求得结果为8,为定值,进而原式得证.
,yo2=4xo-8代入整理求得结果为8,为定值,进而原式得证.解答:
 解:(Ⅰ)抛物线方程中p=4,
解:(Ⅰ)抛物线方程中p=4,∴焦点坐标为(2,0),准线方程为x=-2
(Ⅱ)设A(x1,y1),B(x2,y2),AB中点E(xo,yo),焦点F(2,0).
则有x1+x2=2xo,y1+y2=2yo,又A,B在曲线上有y12=8x1,y22=8x2,
两式相减得AB斜率k=
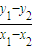 =
=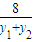 =
= =tana,得yotana=4.
=tana,得yotana=4.又AB,MP共线,易得AB中垂线方程y=-
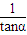 (x-xo)+yo,令y=0,
(x-xo)+yo,令y=0,得P点横坐标xP=xo+yotana=xo+4.
于是得|FP|=xP-xF=xo+2.
由于1-cos2a=1-(cos2a-sin2a)=1-
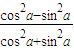 =1-(1-
=1-(1-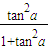 ),
),再将tana=
 ,yo2=4xo-8代入整理得1-cos2a=
,yo2=4xo-8代入整理得1-cos2a=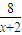 ,
,从而有|PF|-|PF|cos2a=|PF|(1-cos2a)=(xo+2)
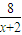 =8.
=8.原式得证.
点评:本题主要考查了抛物线的应用,平面解析式的基础知识.考查了考生的基础知识的综合运用和知识迁移的能力.

练习册系列答案
相关题目
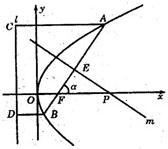 如图,倾斜角为a的直线经过抛物线y2=8x的焦点F,且于抛物线交于A、B两点.
如图,倾斜角为a的直线经过抛物线y2=8x的焦点F,且于抛物线交于A、B两点.