题目内容
一个正四棱锥的底面面积为Q,则它的中截面(过各侧棱的中点的截面)的边长是( )
分析:由已知中棱锥的底面面积是Q,根据棱锥的中截面与底面是相似图形,面积比等于相似比的平方,结合棱锥的中截面过棱锥高的中点,确定相似比后,即可得到答案.
解答:解:由棱锥的几何特征可得
棱锥的中截面与棱锥的底面是相似图形
且相似比为
则棱锥的中截面与棱锥的底面的面积之比为相似比的平方
又∵棱锥的底面面积是Q,
∴棱锥的中截面面积是
,则它的中截面的边长是
故选A.
棱锥的中截面与棱锥的底面是相似图形
且相似比为
| 1 |
| 2 |
则棱锥的中截面与棱锥的底面的面积之比为相似比的平方
| 1 |
| 4 |
又∵棱锥的底面面积是Q,
∴棱锥的中截面面积是
| Q |
| 4 |
| ||
| 2 |
故选A.
点评:本题考查的知识点是棱锥的结构特征,相似形的性质,其中根据棱锥的几何特征判断出棱锥的中截面与棱锥的底面是相似图形,将空间问题转化为平面问题是解答本题的关键.

练习册系列答案
相关题目
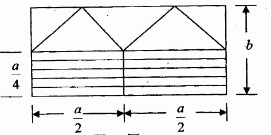 如图是边长分别为a、b的矩形,按图中实线切割后,将它们作为一个正四棱锥的底面(由阴影部分拼接而成)和侧面,则
如图是边长分别为a、b的矩形,按图中实线切割后,将它们作为一个正四棱锥的底面(由阴影部分拼接而成)和侧面,则
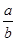 的取值范围是
。
的取值范围是
。