��Ŀ����
��ͼ��ʾ��ͼ(1)��ӳ����ij������������·��֧���y��˿���x֮���ϵ��ͼ������Ŀǰ����������·���𣬹�˾�й���Ա������ֵ������飬��ͼ(2)(3)��ʾ��
(ע����֧��Ӫҵ���õ�Ʊ�����룭�����ijɱ�)
��������˵����
��ͼ(2)�Ľ����ǣ���߳ɱ��������Ʊ�ۣ�
��ͼ(2)�Ľ����ǣ����ͳɱ���������Ʊ�۲��䣻
��ͼ(3)�Ľ����ǣ����Ʊ�ۣ������ֳɱ����䣻
��ͼ(3)�Ľ����ǣ����Ʊ�ۣ������ͳɱ���
����˵����ȷ�������(����)
| A���٢� | B���٢� | C���ڢ� | D���ڢ� |
C
����

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
���ں��� ����
���� Ϊijһ�����ε����߳������
Ϊijһ�����ε����߳������ Ϊ���ɹ��������κ���������֪����
Ϊ���ɹ��������κ���������֪���� �ǡ��ɹ��������κ���������ʵ��t��ȡֵ��Χ�ǣ� ��
�ǡ��ɹ��������κ���������ʵ��t��ȡֵ��Χ�ǣ� ��
A�� | B�� | C�� | D�� |
��֪����y=f(x)����:�������x1<x2��-1,[f(x2)-f(x1)](x2-x1)>0�����,��f(-2),f(- ),f(-1)�Ĵ�С��ϵΪ(����)
),f(-1)�Ĵ�С��ϵΪ(����)
A��f(-2)<f(- )<f(-1) )<f(-1) |
B��f(-2)>f(- )>f(-1) )>f(-1) |
C��f(-2)>f(-1)>f(- ) ) |
D��f(- )>f(-2)>f(-1) )>f(-2)>f(-1) |
����f(x)��1��xlog2x��������ڵ�������(����)
A�� �� �� | B�� ��1 ��1 | C��(1��2) | D��(2��3) |
��֪����f(x)�� (k��R)��������y��|f(x)|��k��������㣬��ʵ��k��ȡֵ��Χ��(����)
(k��R)��������y��|f(x)|��k��������㣬��ʵ��k��ȡֵ��Χ��(����)
| A��k��2 | B����1<k<0 | C����2��k<��1 | D��k�ܣ�2 |
 ��ͼ��Ϊ�� ��
��ͼ��Ϊ�� ��
 �Ķ�����Ϊ________��
�Ķ�����Ϊ________��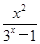 ��ͼ������� (����)��
��ͼ������� (����)��
 ��Ӧ�������д��ڡ��Թ����ߡ�����(����)��
��Ӧ�������д��ڡ��Թ����ߡ�����(����)��