题目内容
用两种方法说明函数y=tan(
x-
)的图象可以由函数y=tanx的图象经过怎样的变换得到.
| 1 |
| 2 |
| π |
| 6 |
分析:法(1)先进行周期变换,再进行相位变换;
法(2)先进行相位变换,再进行周期变换.
法(2)先进行相位变换,再进行周期变换.
解答:解:法(1)y=tanx横坐标变为原来的2倍,得到y=tan
x的图象,再将y=tan
x的图象向右平移
个单位,得到y=tan
(x-
)=tan(
x-
)的图象.(6分)
法(2)y=tanx向右平移
个单位,得到y=tan(x-
)的图象,再将y=tan(x-
)的图象的横坐标变为原来的2倍(纵坐标不变)得到y=tan(
x-
)的图象.(6分)
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
法(2)y=tanx向右平移
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
点评:本题考查函数y=Asin(ωx+φ)的图象变换.,着重考查周期变换与相位变换,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
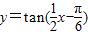 的图象可以由函数y=tanx的图象经过怎样的变换得到.
的图象可以由函数y=tanx的图象经过怎样的变换得到.