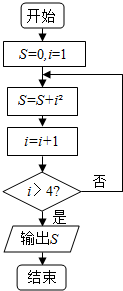
题目内容
17.化简:(1)$\frac{cos(180°+α)sin(90°+α)tan(α+360°)}{sin(-α-180°)cos(-180°-α)cos(270°-α)}$.
(2)$\frac{1}{cosα\sqrt{1+ta{n}^{2}α}}$+$\sqrt{\frac{1+sinα}{1-sinα}}$-$\sqrt{\frac{1-sinα}{1+sinα}}$(其中α为第二象限角).
分析 (1)利用诱导公式及同角三角函数基本关系式即可化简得解;
(2)根据α的范围可求cosα<0,利用诱导公式及同角三角函数基本关系式即可化简得解;
解答 解:(1)原式=$\frac{{-cosα•cosα•\frac{sinα}{cosα}}}{{sinα•({-cosα})•({-sinα})}}=-\frac{1}{sinα}$.
(2)∵α为第二象限角,cosα<0,
∴原式=$\frac{1}{cosα×\sqrt{\frac{1}{co{s}^{2}α}}}$+$\sqrt{\frac{(1+sinα)^{2}}{co{s}^{2}α}}$-$\sqrt{\frac{(1-sinα)^{2}}{co{s}^{2}α}}$=$-1+\frac{1+sinα}{-cosα}+\frac{1-sinα}{cosα}=-1-2tanα$.
点评 本题主要考查了诱导公式及同角三角函数基本关系式的应用,属于基础题.

练习册系列答案
相关题目