题目内容
已知椭圆C的中心为O,左焦点为F(-1,0),且过点(
,
).
(1)求椭圆C的方程;
(2)若点P为椭圆上的任意一点,求
•
的最大值.
| 3 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)若点P为椭圆上的任意一点,求
| OP |
| FP |
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:计算题,平面向量及应用,圆锥曲线的定义、性质与方程
分析:(1)设椭圆的方程为:
+
=1(a>b>0),则c=1,即a2-b2=1,
+
=1,解出即可得到;
(2)设P(2cosα,
sinα),运用向量的数量积的坐标公式,化简配方,再由余弦函数的图象和性质,即可得到最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| a2 |
| 3 |
| 4b2 |
(2)设P(2cosα,
| 3 |
解答:
解:(1)设椭圆的方程为:
+
=1(a>b>0),
则c=1,即a2-b2=1,
+
=1,
解得,a2=4,b2=3,
则椭圆方程为:
+
=1;
(2)设P(2cosα,
sinα),
则
•
=(2cosα,
sinα)•(2cosα+1,
sinα),
=2cosα(2cosα+1)+3sin2α=cos2α+2cosα+3,
=(cosα+1)2+2,由于-1≤cosα≤1,
则cosα=1时,取得最大值,且为6.
| x2 |
| a2 |
| y2 |
| b2 |
则c=1,即a2-b2=1,
| 3 |
| a2 |
| 3 |
| 4b2 |
解得,a2=4,b2=3,
则椭圆方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(2)设P(2cosα,
| 3 |
则
| OP |
| FP |
| 3 |
| 3 |
=2cosα(2cosα+1)+3sin2α=cos2α+2cosα+3,
=(cosα+1)2+2,由于-1≤cosα≤1,
则cosα=1时,取得最大值,且为6.
点评:本题考查椭圆的方程和性质,考查平面向量的数量积的坐标表示及三角函数的图象和性质,考查运算能力,属于中档题.

练习册系列答案
相关题目
一个物体的运动方程为s=-
t3+2t2-5,其中s的单位是米,t的单位是秒,那么物体在3秒末的瞬时速度是( )
| 1 |
| 3 |
| A、3米/秒 | B、6米/秒 |
| C、5米/秒 | D、4米/秒 |
在等差数列{an}中,已知a1+a2=4,a2+a3=8,则a7等于( )
| A、7 | B、10 | C、13 | D、19 |
非零实数x、y、z成等差数列,x+1、y、z与x、y、z+2均成等比数列,则y等于( )
| A、16 | B、14 | C、12 | D、10 |
设A={x∈N|1≤x<6},则下列正确的是( )
| A、6∈A | B、0∈A |
| C、3?A | D、3.5∉a |
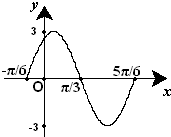 已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的一段图象(如图)所示.
已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的一段图象(如图)所示.