题目内容
(本小题满分15分)
某人准备购置一块占地1800平方米的矩形地块,中间建三个矩形温室大棚,大棚周围均是宽为1米的小路(阴影部分所示),大棚所占地面积为S平方米,其中a∶b=1∶2.
(1)试用x,y表示S;
(2)若要使S最大,则x,y的值各为多少?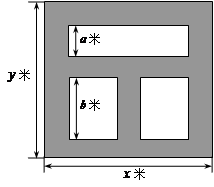
某人准备购置一块占地1800平方米的矩形地块,中间建三个矩形温室大棚,大棚周围均是宽为1米的小路(阴影部分所示),大棚所占地面积为S平方米,其中a∶b=1∶2.
(1)试用x,y表示S;
(2)若要使S最大,则x,y的值各为多少?

(1)S=1808-3x- y.(2)当x=40,y=45时,S取得最大值.
y.(2)当x=40,y=45时,S取得最大值.
 y.(2)当x=40,y=45时,S取得最大值.
y.(2)当x=40,y=45时,S取得最大值. 本试题主要是考察了函数在实际生活中的运用,借助于不等式的思想或者是函数单调性的思想,求解最值的实际应用。
(1)根据已知条件,设出变量,然后借助于面积关系,得到解析式。
(2)根据第一问中的结论,分析函数的性质,或者运用均值不等式的思想,求解得到最值。
解: (1)由题可得:xy=1800,b=2a
则y=a+b+3=3a+3, ··········· 4分
S=(x-2)a +(x-3)b=(3x-8)a=(3x-8) =1808-3x-
=1808-3x- y. ········ 8分
y. ········ 8分
(2) S=1808-3x- y=1808-3x-
y=1808-3x- ×
× =1808-3 (x+
=1808-3 (x+ ) ······· 10分
) ······· 10分
≤1808-3×2 =1808-240=1568, ·········· 12分
=1808-240=1568, ·········· 12分
当且仅当x= ,即x=40时取等号,S取得最大值.此时y=
,即x=40时取等号,S取得最大值.此时y= =45,
=45,
所以当x=40,y=45时,S取得最大值. 15分
(1)根据已知条件,设出变量,然后借助于面积关系,得到解析式。
(2)根据第一问中的结论,分析函数的性质,或者运用均值不等式的思想,求解得到最值。
解: (1)由题可得:xy=1800,b=2a
则y=a+b+3=3a+3, ··········· 4分
S=(x-2)a +(x-3)b=(3x-8)a=(3x-8)
 =1808-3x-
=1808-3x- y. ········ 8分
y. ········ 8分(2) S=1808-3x-
 y=1808-3x-
y=1808-3x- ×
× =1808-3 (x+
=1808-3 (x+ ) ······· 10分
) ······· 10分≤1808-3×2
 =1808-240=1568, ·········· 12分
=1808-240=1568, ·········· 12分当且仅当x=
 ,即x=40时取等号,S取得最大值.此时y=
,即x=40时取等号,S取得最大值.此时y= =45,
=45,所以当x=40,y=45时,S取得最大值. 15分

练习册系列答案
相关题目
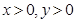 且
且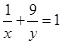 ,求
,求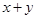 的最小值
的最小值 则恒有( )
则恒有( ) 



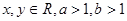 ,若
,若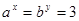 ,
,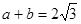 ,则
,则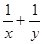 的最大值是
的最大值是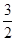
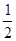
 ,且
,且 ,则
,则 的最小值为___________.
的最小值为___________. 满足:
满足: ,则
,则 的最大值为 .
的最大值为 . ,且
,且 ,
, ,则
,则 的值等于 ( )
的值等于 ( )
 满足
满足 ,则( )
,则( ) 有最大值4
有最大值4  有最小值
有最小值
 有最大值
有最大值
 有最小值
有最小值
 且
且 ,则
,则 的最小值为( )
的最小值为( )


