题目内容
△ABC中，三边长分别为10，5
，5(1+
)，则此三角形最长边上的高为 ．
| 2 |
| 3 |
分析：先利用余弦定理求出最大角的余弦，进而可得正弦，利用三角形的面积公式建立等式，即可求得结论．
解答：解：设最大角为α，三角形最长边上的高为h，则cosα=
=
，
∴sinα=
=
，
∴S△ABC=
•10•5
•
=
•5(1+
)h，
∴h=5．
故答案为：5．
102+(5
| ||||
2•10•5
|
1-
| ||
2
|
∴sinα=
| 1-cos2α |
1+
| ||
2
|
∴S△ABC=
| 1 |
| 2 |
| 2 |
1+
| ||
2
|
| 1 |
| 2 |
| 3 |
∴h=5．
故答案为：5．
点评：本题考查余弦定理的运用，考查三角形面积的计算，正确运用三角形的面积公式是关键．
练习册系列答案
阅读快车系列答案
相关题目
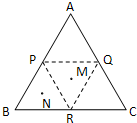正三角形ABC边长为2，P，Q，R，分别是三边的中点，把△APQ，△BPR，△CQR分别沿PQ，PR，QR折起，使得A，B，C重合，M，N分别是△PQR，△BPR的中心，则在几何体中MN的长是