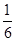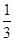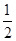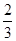题目内容
在画两个变量的散点图时，下面哪个叙述是正确的( )
| A．预报变量在x轴上，解释变量在y轴上 | B．解释变量在x轴上，预报变量在y轴上 |
| C．可以选择两个变量中任意一个在x轴上 | D．以选择两个变量中任意一个在y轴上 |
B
解析试题分析：因为回归分析的目的是研究解释变量对预报变量影响的大小和关系的，故解释变量为自变量，预报变量为因变量. 解：∵通常把自变量称为解析变量，因变量称为预报变量，∴故解释变量为自变量，预报变量为因变量．故选B
考点：散点图
点评：本题主要考查散点图，考查回归分析的目的是研究解释变量对预报变量影响的大小和关系的．
练习册系列答案
相关题目
2012年学期末，某学校对100间学生公寓进行综合评比，依考核分数分为A,B,C,D四种等级，其中分数在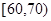
为D等级，有15间；分数在
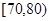为C等级，有40间；分数在
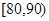为B等级，有20间；分数在
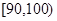为D等级，有25间. 考核评估后，得其频率直方图如图所示，估计这100间学生公寓评估得分的中位数是
| A．78.65 | B．78.75 | C．78.80 | D．78.85 |
在样本的频率分布直方图中, 共有9个小长方形, 若第一个长方形的面积为0.02, 前五个与后五个长方形的面积分别成等差数列且公差互为相反数,若样本容量为160, 则中间一组（即第五组）的频数为（ ）
| A．12 | B．24 | C．36 | D．48 |
以下有关线性回归分析的说法不正确的是( )
A．通过最小二乘法得到的线性回归直线经过样本的中心 |
B．用最小二乘法求回归直线方程，是寻求使 最小的a,b的值 |
| C．相关系数r越小，表明两个变量相关性越弱 |
D． 越接近1，表明回归的效果越好 |
在两个变量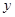
与
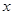的回归模型中，分别选择了4个不同模型，它们的相关指数
如下，其中拟和效果最好的模型是（ ）
| A．模型1的相关指数为0.25 | B．模型2的相关指数为0.50 |
| C．模型3的相关指数为0.98 | D．模型4的相关指数为0.80 |
在建立两个变量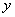
与
的回归模型中，分别选择了4个不同的模型，它们的相关指数
如下，其中拟合最好的模型是（ ）
| A．模型1的相关指数为0.98 | B．模型2的相关指数为0.80 |
| C．模型3的相关指数为0.50 | D．模型4的相关指数为0.25 |
一个容量为35的样本数据，分组后，组距与频数如下：
个；
个；
个；
个；
个；
个。则样本在区间
上的频率为
| A．20% | B．69% | C．31% | D．27% |
随机抽取某中学甲、乙两面个班10名同学，测量他们的身高（单位：cm）后获得身高数据的茎叶图如图甲所示，在这20人中，记身高在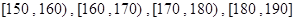
内的人数依次为
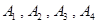，图乙是统计样本中身高在一定范围内的人数的算法流程图，则下列说法正确的是（ ）
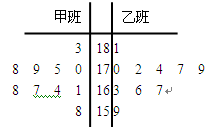
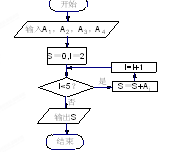
| A．由图甲可知甲、乙两班中身高的中位数较大的是甲班，图乙输出的S的值为18 |
| B．由图甲可知甲、乙两班中身高的中位数较大的是乙班，图乙输出的S的值为18 |
| C．由图甲可知甲、乙两班中身高的中位数较大的是乙班，图乙输出的S的值为16 |
| D．由图甲可知甲、乙两班中身高的中位数较大的是甲班，图乙输出的S的值为16 |
