题目内容
已知数列{an},如果数列{bn}满足 ,则称数列{bn}是数列{an}的“生成数列”
,则称数列{bn}是数列{an}的“生成数列”(1)若数列{an}的通项为an=n,写出数列{an}的“生成数列”{bn}的通项公式;
(2)若数列{cn}的通项为cn=2n+b,(其中b是常数),试问数列{cn}的“生成数列”{ln}是否是等差数列,请说明理由.
(3)已知数列{dn}的通项为
 ,设数列{dn}的“生成数列”{pn}的前n项和为Tn,问是否存在自然数m满足满足(Tm-2012)(Tm-6260)≤0,若存在请求出m的值,否则请说明理由.
,设数列{dn}的“生成数列”{pn}的前n项和为Tn,问是否存在自然数m满足满足(Tm-2012)(Tm-6260)≤0,若存在请求出m的值,否则请说明理由.
【答案】分析:(1)根据“生成数列”的定义,数列{bn}满足 ,结合数列{an}的通项为an=n,递推可得结论;
,结合数列{an}的通项为an=n,递推可得结论;
(2)根据“生成数列”的定义,结合数列{cn}的通项为cn=2n+b,(其中b是常数),求出数列{cn}的“生成数列”{ln},利用等差数列的定义判断后可得结论;
(3)根据“生成数列”的定义,结合数列{dn}的通项为 ,求出数列{dn}的“生成数列”{pn}的前n项和为Tn,解不等式可得m的值.
,求出数列{dn}的“生成数列”{pn}的前n项和为Tn,解不等式可得m的值.
解答:解:(1)∵数列{bn}满足 ,
,
数列{an}的通项为an=n,
∴ 3分
3分
综合得:bn=2n-14分
(2) 6分
6分
当b=0时,ln=4n-2,由于ln+1-ln=4(常数)
所以此时数列{cn}的“生成数列”{ln}是等差数列 8分
当b≠0时,由于c1=2+b,c2=6+2b,c3=10+2b,9分
此时c1+c3≠2c2,
∴此时数列{cn}的“生成数列”{ln}不是等差数列. 10分
(3) 11分
11分
当n=1时,Tn=p1=312分
当n≥2时
=3+(3•2+3•22+…+3•2n-1)+(3+5+…+2n-1)
=3•2n+n2-4,14分
所以 ,15分
,15分
若(Tm-2012)(Tm-6260)≤0,则2012≤Tn≤626016分
由于{Tn}对于一切自然数是增函数,
T9=1613<2012,T10=3168>2013T11=6261>6260
所以存在唯一的自然数m=10满足若(Tm-2012)(Tm-6260)≤0成立 18分.
点评:本题考查的知识识是数列与不等式,等差关系的确定,数列的递推式,是数列知识较为综合的应用,还涉及新定义,较难理解,属于难题.
 ,结合数列{an}的通项为an=n,递推可得结论;
,结合数列{an}的通项为an=n,递推可得结论;(2)根据“生成数列”的定义,结合数列{cn}的通项为cn=2n+b,(其中b是常数),求出数列{cn}的“生成数列”{ln},利用等差数列的定义判断后可得结论;
(3)根据“生成数列”的定义,结合数列{dn}的通项为
 ,求出数列{dn}的“生成数列”{pn}的前n项和为Tn,解不等式可得m的值.
,求出数列{dn}的“生成数列”{pn}的前n项和为Tn,解不等式可得m的值.解答:解:(1)∵数列{bn}满足
 ,
,数列{an}的通项为an=n,
∴
 3分
3分综合得:bn=2n-14分
(2)
 6分
6分当b=0时,ln=4n-2,由于ln+1-ln=4(常数)
所以此时数列{cn}的“生成数列”{ln}是等差数列 8分
当b≠0时,由于c1=2+b,c2=6+2b,c3=10+2b,9分
此时c1+c3≠2c2,
∴此时数列{cn}的“生成数列”{ln}不是等差数列. 10分
(3)
 11分
11分当n=1时,Tn=p1=312分
当n≥2时

=3+(3•2+3•22+…+3•2n-1)+(3+5+…+2n-1)
=3•2n+n2-4,14分
所以
 ,15分
,15分若(Tm-2012)(Tm-6260)≤0,则2012≤Tn≤626016分
由于{Tn}对于一切自然数是增函数,
T9=1613<2012,T10=3168>2013T11=6261>6260
所以存在唯一的自然数m=10满足若(Tm-2012)(Tm-6260)≤0成立 18分.
点评:本题考查的知识识是数列与不等式,等差关系的确定,数列的递推式,是数列知识较为综合的应用,还涉及新定义,较难理解,属于难题.

练习册系列答案
相关题目
 已知数列{an}满足如图所示的程序框图.
已知数列{an}满足如图所示的程序框图. 已知数列{an}满足如图所示的流程图
已知数列{an}满足如图所示的流程图 已知数列{an}满足如图所示的程序框图.
已知数列{an}满足如图所示的程序框图.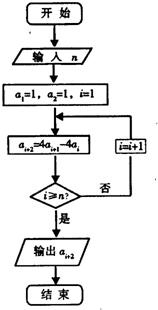 已知数列{an}满足如图所示的程序框图.
已知数列{an}满足如图所示的程序框图. 是等差数列,并求{an}的通项公式.
是等差数列,并求{an}的通项公式.