题目内容
已知数列{bn}中,b1=1,且点(bn+1,bn)在直线y=x-1上.数列{an}中,a1=1,an+1=2an+3,
(Ⅰ) 求数列{bn}的通项公式
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)若cn=an+3,求数列{bncn}的前n项和Sn.
(Ⅰ) 求数列{bn}的通项公式
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)若cn=an+3,求数列{bncn}的前n项和Sn.
分析:(Ⅰ)利用点(bn+1,bn)在直线y=x-1上,确定数列{bn}是以1为首项,1为公差的等差数列,可求数列{bn}的通项公式;
(Ⅱ)根据数列递推式an+1=2an+3,可得an+1+3=2(an+3),从而可得{an+3}是以4为首项,2为公比的等比数列,由此可求数列{an}的通项公式;
(Ⅲ)确定数列的通项,利用错位相减法,可得数列{bncn}的前n项和Sn.
(Ⅱ)根据数列递推式an+1=2an+3,可得an+1+3=2(an+3),从而可得{an+3}是以4为首项,2为公比的等比数列,由此可求数列{an}的通项公式;
(Ⅲ)确定数列的通项,利用错位相减法,可得数列{bncn}的前n项和Sn.
解答:解:(Ⅰ)∵点(bn+1,bn)在直线y=x-1上,∴bn+1-bn=1
∵b1=1,∴数列{bn}是以1为首项,1为公差的等差数列
∴bn=n(n∈N*);
(Ⅱ)∵an+1=2an+3,∴an+1+3=2(an+3)
∵a1=1,∴a1+3=4
∴{an+3}是以4为首项,2为公比的等比数列
∴an+3=4×2n-1=2n+1,
∴an=2n+1-3(n∈N*);
(Ⅲ)cn=an+3=2n+1,∴bncn=n×2n+1,
∴Sn=1×22+2×23+…+n×2n+1,①
∴2Sn=1×23+2×24+…+n×2n+2,②
①-②可得:-Sn=1×22+1×23+…+1×2n+1-n×2n+2
∴Sn=(n-1)•2n+2+4(n∈N*)
∵b1=1,∴数列{bn}是以1为首项,1为公差的等差数列
∴bn=n(n∈N*);
(Ⅱ)∵an+1=2an+3,∴an+1+3=2(an+3)
∵a1=1,∴a1+3=4
∴{an+3}是以4为首项,2为公比的等比数列
∴an+3=4×2n-1=2n+1,
∴an=2n+1-3(n∈N*);
(Ⅲ)cn=an+3=2n+1,∴bncn=n×2n+1,
∴Sn=1×22+2×23+…+n×2n+1,①
∴2Sn=1×23+2×24+…+n×2n+2,②
①-②可得:-Sn=1×22+1×23+…+1×2n+1-n×2n+2
∴Sn=(n-1)•2n+2+4(n∈N*)
点评:本题考查数列递推式,考查数列通项的确定,考查数列的求和,确定数列是等差数列与等比数列是解题的关键.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 ,
, ,数列{an}满足:
,数列{an}满足: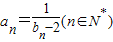 .
.