题目内容
已知数列{bn}中, ,
, ,数列{an}满足:
,数列{an}满足: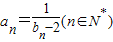 .
.(1)求a1,a2;
(2)求证:an+1+2an+1=0;
(3)求数列{an}的通项公式;
(4)求证:(-1)b1+(-1)2b2+…+(-1)nbn<1(n∈N*)
【答案】分析:(1)根据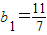 ,求得
,求得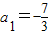 ,从而
,从而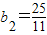
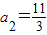 ;
;
(2)将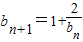 代入得到:
代入得到: 即可证得:an+1+2an+1=0;
即可证得:an+1+2an+1=0;
(3)由(2)所得结论变形得到: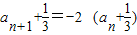 从而得出数列
从而得出数列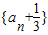 是以-2为首项,公比为-2的等比数列,最后利用等比数列的通项公式即可求出数列{an}的通项公式;
是以-2为首项,公比为-2的等比数列,最后利用等比数列的通项公式即可求出数列{an}的通项公式;
(4)由(3)得出数列{an}的通项公式写出数列bn,下面对n进行奇偶数讨论:①当n为偶数时②当n为奇数时,分别利用等比数列的前n项结合不等式的放缩即可得到证明.
解答:解:(1)∵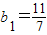 ∴
∴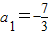 ∴
∴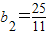
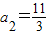 …(3分)
…(3分)
(2)证明:∵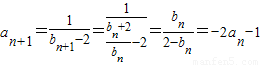 ∴an+1+2an+1=0…(5分)
∴an+1+2an+1=0…(5分)
(3)∵an+1=-2an-1∴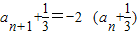 …(6分)
…(6分)
又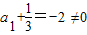 ∴数列
∴数列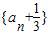 是以-2为首项,公比为-2的等比数列…(7分)
是以-2为首项,公比为-2的等比数列…(7分)
∴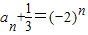 ∴
∴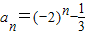 …(8分)
…(8分)
(4)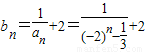 ∴
∴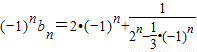
当n为奇数时(-1)nbn+(-1)n+1bn+1=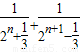 =
=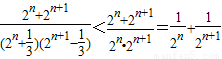 ,
,
①当n为偶数时,(-1)b1+(-1)2b2+…+(-1)nbn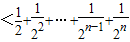
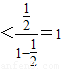 ,
,
②当n为奇数时,(-1)b1+(-1)2b2+…+(-1)nbn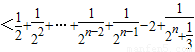
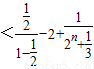 =
=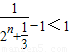 …(11分)
…(11分)
综上所述:(-1)b1+(-1)2b2+…+(-1)nbn<1…(12分)
点评:本小题主要考查数列递推式、数列与不等式的综合、不等式的性质等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
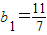 ,求得
,求得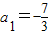 ,从而
,从而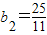
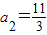 ;
;(2)将
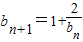 代入得到:
代入得到: 即可证得:an+1+2an+1=0;
即可证得:an+1+2an+1=0;(3)由(2)所得结论变形得到:
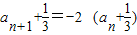 从而得出数列
从而得出数列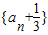 是以-2为首项,公比为-2的等比数列,最后利用等比数列的通项公式即可求出数列{an}的通项公式;
是以-2为首项,公比为-2的等比数列,最后利用等比数列的通项公式即可求出数列{an}的通项公式;(4)由(3)得出数列{an}的通项公式写出数列bn,下面对n进行奇偶数讨论:①当n为偶数时②当n为奇数时,分别利用等比数列的前n项结合不等式的放缩即可得到证明.
解答:解:(1)∵
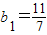 ∴
∴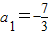 ∴
∴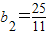
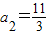 …(3分)
…(3分)(2)证明:∵
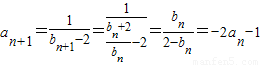 ∴an+1+2an+1=0…(5分)
∴an+1+2an+1=0…(5分)(3)∵an+1=-2an-1∴
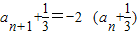 …(6分)
…(6分)又
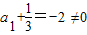 ∴数列
∴数列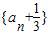 是以-2为首项,公比为-2的等比数列…(7分)
是以-2为首项,公比为-2的等比数列…(7分)∴
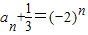 ∴
∴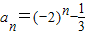 …(8分)
…(8分)(4)
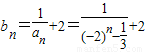 ∴
∴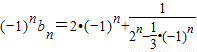
当n为奇数时(-1)nbn+(-1)n+1bn+1=
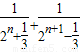 =
=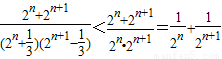 ,
,①当n为偶数时,(-1)b1+(-1)2b2+…+(-1)nbn
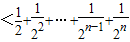
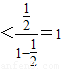 ,
,②当n为奇数时,(-1)b1+(-1)2b2+…+(-1)nbn
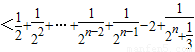
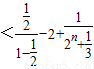 =
=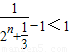 …(11分)
…(11分)综上所述:(-1)b1+(-1)2b2+…+(-1)nbn<1…(12分)
点评:本小题主要考查数列递推式、数列与不等式的综合、不等式的性质等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目