题目内容
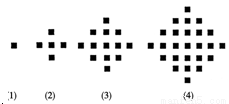
(本题满分12分)某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1)求出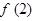 ,
,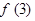
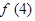
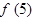 并猜测
并猜测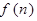 的表达式;
的表达式;
(2)求证:+++…+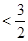 .
.
解: (1)∵ f(1)=1,f(2)=5,f(3)=13,f(4)=25,∴ f(5)=25+4×4=41.
∵ f(2)-f(1)=4=4×1,f(3)-f(2)=8=4×2,f(4)-f(3)=12=4×3,f(5)-f(4)=16=4×4,
f(n)=2n2-2n+1.
(2)当n≥2时,==,
∴ +++…+
=1+
=1+=- .
.
【解析】本试题主要是考查了数列的归纳猜想思想的运用,根据前几项。来猜想并运用数学归纳法加以证明。
(1)结合题目中的 递推关系式可知前几项的值,并猜想结论。
(2)分为两步骤进行,先证明n取第一个值时成立,再假设n=k时成立,证明n=k+1时也成立即可。
解: (1)∵ f(1)=1,f(2)=5,f(3)=13,f(4)=25,∴ f(5)=25+4×4=41.
∵ f(2)-f(1)=4=4×1,f(3)-f(2)=8=4×2,f(4)-f(3)=12=4×3,f(5)-f(4)=16=4×4,
由上式规律得出f(n+1)-f(n)=4n. ∴ f(n)-f(n-1)=4(n-1),f(n-1)-f(n-2)=4·(n-2),
f(n-2)-f(n-3)=4·(n-3),…
f(2)-f(1)=4×1,
∴ f(n)-f(1)=4[(n-1)+(n-2)+…+2+1]=2(n-1)·n,∴ f(n)=2n2-2n+1(n≥2),
又n=1时,f(1)也适合f(n).
∴ f(n)=2n2-2n+1. --------6分
(2)当n≥2时,==,
∴ +++…+[来源:Z,xx,k.Com]
=1+
=1+=- . ---------------12分
. ---------------12分

 优加精卷系列答案
优加精卷系列答案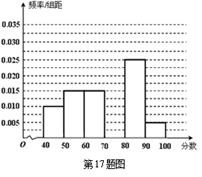
 ,
, ,…,
,…,  后得到如下频率分布直方图.
后得到如下频率分布直方图.
 内的频率;
内的频率; 两型会议桌,每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套
两型会议桌,每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套 的厂房(不管墙高),工程的造价是:
的厂房(不管墙高),工程的造价是: