题目内容
(本题满分12分)某学校校办工厂有毁坏的房屋一座,留有一面14m的旧墙,现准备利用这面墙的一段为面墙,建造平面图形为矩形且面积为126 的厂房(不管墙高),工程的造价是:
的厂房(不管墙高),工程的造价是:
(1)修1m旧墙的费用是造1m新墙费用的25%;
(2)拆去1m旧墙用所得的材料来建1m新墙的费用是建1m新墙费用的50%.
问如何利用旧墙才能使建墙的费用最低?
【答案】
保留12 m的旧墙时总费用为最低
【解析】解: 设保留旧墙x m,即拆去旧墙(14-x)m修新墙,设建1m新墙费用为a元,则修旧墙的费用为y
 =25%
=25% ax=
ax=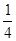 ax; 拆旧墙建新墙的费用为y
ax; 拆旧墙建新墙的费用为y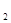 =(14-x)
=(14-x)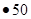 %a=
%a=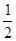 a(14-x);建新墙的费用为:y
a(14-x);建新墙的费用为:y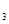 =(
=(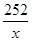 +2x-14)a.
+2x-14)a.
于是,所需的总费用为:
y=y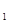 + y
+ y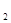 + y
+ y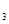
=[(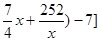 a
a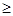 [2
[2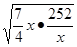
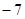 ]a=35a,
]a=35a,
当且仅当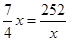 ,即x=12时上式的“=”成立;
,即x=12时上式的“=”成立;
故保留12 m的旧墙时总费用为最低。

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
 ,
, ,…,
,…, 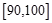 后得到如下频率分布直方图.
后得到如下频率分布直方图.
 内的频率;
内的频率; 两型会议桌,每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套
两型会议桌,每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套