题目内容
已知集合A={x|(x-2)[x-(3a+1)]<0},集合B={x|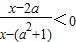 }.
}.(1)a=2时,求A∩B;
(2)a
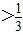 时,若A∩B=B,求实a的取值范围.
时,若A∩B=B,求实a的取值范围.
【答案】分析:(1)已知a=2,解A,B所含方程组成的不等式组即可求得A∩B;
(2)已知A∩B=B得B⊆A,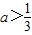 得3a+1>2,可求解集合A,讨论2a和a2+1的大小关系,解集合B,根据B⊆A确定a的取值范围.
得3a+1>2,可求解集合A,讨论2a和a2+1的大小关系,解集合B,根据B⊆A确定a的取值范围.
解答:解:(1)a=2时,解方程组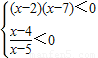 得,4<x<5,
得,4<x<5,
故A∩B={x|4<x<5}
(2)已知A∩B=B得B⊆A,
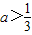 时,3a+1>2,A={x|(x-2)[x-(3a+1)]<0}={x|2<x<3a+1}
时,3a+1>2,A={x|(x-2)[x-(3a+1)]<0}={x|2<x<3a+1}
讨论2a和a2+1的大小关系:
①若a2+1=2a得a=1,即1<0不成立,集合B为空集,A={x|2<x<4},满足B⊆A
②若a2+1>2a得a≠1,B={x|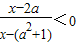 }={x|2a<x<a2+1},∵B⊆A
}={x|2a<x<a2+1},∵B⊆A
∴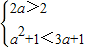 解得1<a<3
解得1<a<3
③若a2+1<2a即(a-1)2<0,这样的a不存在
综上所述,实数a的取值范围为{a|1≤a<3}.
点评:本题考查集合的并集运算,(1)实质为解不等式组,较简单;(2)需要进行分类讨论,注意a2+1>2a时的计算要根据B⊆A得出正确的不等式组,不要混淆大小关系,分类讨论时还应注意不能遗漏,本题属于难题,易错题.
(2)已知A∩B=B得B⊆A,
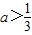 得3a+1>2,可求解集合A,讨论2a和a2+1的大小关系,解集合B,根据B⊆A确定a的取值范围.
得3a+1>2,可求解集合A,讨论2a和a2+1的大小关系,解集合B,根据B⊆A确定a的取值范围.解答:解:(1)a=2时,解方程组
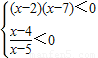 得,4<x<5,
得,4<x<5,故A∩B={x|4<x<5}
(2)已知A∩B=B得B⊆A,
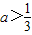 时,3a+1>2,A={x|(x-2)[x-(3a+1)]<0}={x|2<x<3a+1}
时,3a+1>2,A={x|(x-2)[x-(3a+1)]<0}={x|2<x<3a+1}讨论2a和a2+1的大小关系:
①若a2+1=2a得a=1,即1<0不成立,集合B为空集,A={x|2<x<4},满足B⊆A
②若a2+1>2a得a≠1,B={x|
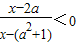 }={x|2a<x<a2+1},∵B⊆A
}={x|2a<x<a2+1},∵B⊆A ∴
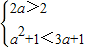 解得1<a<3
解得1<a<3③若a2+1<2a即(a-1)2<0,这样的a不存在
综上所述,实数a的取值范围为{a|1≤a<3}.
点评:本题考查集合的并集运算,(1)实质为解不等式组,较简单;(2)需要进行分类讨论,注意a2+1>2a时的计算要根据B⊆A得出正确的不等式组,不要混淆大小关系,分类讨论时还应注意不能遗漏,本题属于难题,易错题.

练习册系列答案
相关题目