题目内容
如图,割线PBC经过圆心O,PB=OB=1,OB绕点O逆时针旋转120°到OD,连结PD交圆O于点E,则PE= 

解析试题分析:法一:连结CD,BE,则 OCD=
OCD= PEB,因为OC=OB,PB=OB=1,所以
PEB,因为OC=OB,PB=OB=1,所以 OCD=60
OCD=60 ,OC=1,即PC=3,又因为
,OC=1,即PC=3,又因为 BOD=120°,OD=OC=1,所以CD=1,PD2=CD2+PC2-2CD·PCcos
BOD=120°,OD=OC=1,所以CD=1,PD2=CD2+PC2-2CD·PCcos OCD=7,即PD=
OCD=7,即PD= ,由
,由 OCD=
OCD= PEB,
PEB,  P=
P= P,可得
P,可得 PEB≌
PEB≌ PCD,所以
PCD,所以 ,即
,即 =
= .
.
法二:由法一可知,PB=1,PC=3,PD= ,由割线定理可得PE·PD=PB·PC,
,由割线定理可得PE·PD=PB·PC,  =
= .
.
考点:1. 割线定理;2.余弦定理;3.相似三角形及其性质.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 作
作 的外接圆
的外接圆 的切线交
的切线交 的延长线于点
的延长线于点 .若
.若 ,
,  ,则
,则 .
. 
 是
是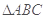 的外接圆,过点C的切线交
的外接圆,过点C的切线交 的延长线于点
的延长线于点 ,
, ,
, 。则
。则 的长___________(2分)AC的长______________(3分).
的长___________(2分)AC的长______________(3分). 
 中,
中, ,
,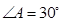 圆
圆 经过
经过 、
、 ,且与
,且与 、
、 分别相交于
分别相交于 .若
.若 ,则圆
,则圆 ________.
________.
 是圆
是圆 的切线,切点为
的切线,切点为 ,
, .
. 是圆
是圆 与圆
与圆 ,
, ,则圆
,则圆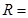 .
. 
 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心,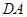 为半径的圆弧与以
为半径的圆弧与以 为直径的圆
为直径的圆 交于点
交于点 ,连接
,连接 并延长
并延长 于
于 .则线段
.则线段 的长为 .
的长为 .

