题目内容
对于给定的正整数n(n≥2),记集合Mn={2,22,23,…,2n}.现将集合Mn的所含有两个元素的子集依次记为Ak(k=1,2,3,…),并将集合Ak中两个元素的积记为ak,所有可能的ak的和记为S.则
(1)若ak的最大值为128,则n=
(2)求S=
(2n-2)(2n-1)
(2n-2)(2n-1)(用n表示).
(1)若ak的最大值为128,则n=
4
4
;(2)求S=
| 4 |
| 3 |
| 4 |
| 3 |
分析:(1)由题意知,ak的最大值为2(n-1)+n=22n-1,根据ak的最大值为128,可求n的值;
(2)由题意,ak可表示为2i•2j(1≤i<j≤m),表示出S,分组求和,即可得到结论.
(2)由题意,ak可表示为2i•2j(1≤i<j≤m),表示出S,分组求和,即可得到结论.
解答:解:(1)由题意知,ak的最大值为2(n-1)+n=22n-1
∵ak的最大值为128,∴22n-1=128,∴n=4;
(2)由题意,ak可表示为2i•2j(1≤i<j≤m),则
S=(21+2+21+3+…+21+n)+(22+3+22+4+…+22+n)+…+2(n-2)+(n-1)+2(n-2)+n)+2(n-1)+n
∵21+(s+1)+22+(s+1)+…+2s+(s+1)=4•(4s-2s)
∴S=4[(4+42+…+4n-1)-(2+22+…+2n-1)]=
(2n-2)(2n-1)
故答案为:4,
(2n-2)(2n-1)
∵ak的最大值为128,∴22n-1=128,∴n=4;
(2)由题意,ak可表示为2i•2j(1≤i<j≤m),则
S=(21+2+21+3+…+21+n)+(22+3+22+4+…+22+n)+…+2(n-2)+(n-1)+2(n-2)+n)+2(n-1)+n
∵21+(s+1)+22+(s+1)+…+2s+(s+1)=4•(4s-2s)
∴S=4[(4+42+…+4n-1)-(2+22+…+2n-1)]=
| 4 |
| 3 |
故答案为:4,
| 4 |
| 3 |
点评:本题考查数列的求和,考查学生分析解决问题的能力,考查分组求和,属于中档题.

练习册系列答案
相关题目
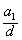 的数值;
的数值;